2023-2024学年北师大版数学八年级上册7.1为什么要证明同步练习（基础卷）

修改时间：2023-12-04 浏览次数：32 类型：同步测试编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 为了证明数轴上的点可以表示无理数，老师给学生设计了如下材料：如图，直径为 $\text{[math]}$ 个单位长度的圆从原点沿数轴向右滚动一周，圆上一点由原点 $\text{[math]}$ 记为点 $\text{[math]}$ 到达点 $\text{[math]}$ ，点 $\text{[math]}$ 对应的数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图，直线 $\text{[math]}$ 被 $\text{[math]}$ 所截， $\text{[math]}$ ，求证： $\text{[math]}$ ．

下列是佳宁同学的证明过程：

证明： $\text{[math]}$

      $\text{[math]}$

      $\text{[math]}$

      $\text{[math]}$

      $\text{[math]}$ （填依据）．

则下列关于上述证明过程中括号内填依据正确的是（）

A . 两直线平行，同位角相等 B . 两直线平行，内错角相等 C . 同位角相等，两直线平行 D . 内错角相等，两直线平行

查看解析收藏纠错

+选题
3. 老师布置了一项作业，对一个真命题进行证明，下面是小云给出的证明过程：
证明：如图， $\text{[math]}$ ，
      $\text{[math]}$ ．
      $\text{[math]}$ ，
      $\text{[math]}$ ，
      $\text{[math]}$ ，
      $\text{[math]}$ ．
已知该证明过程是正确的，则证明的真命题是（）

A . 在同一平面内，若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ B . 在同一平面内，若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ C . 两直线平行，同位角不相等 D . 两直线平行，同位角相等

查看解析收藏纠错

+选题
4. 在探究证明“三角形的内角和是180°”时，综合实践小组的同学作了如下四种辅助线，其中不能证明“三角形内角和是180°”的是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的边 $\text{[math]}$ 上的中线，那么可以证明 $\text{[math]}$ ≌ $\text{[math]}$ ，这里证明全等所使用的判定方法是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 用直尺和圆规作一个角等于已知角的示意图如下，则要说明 $\text{[math]}$ ，需要证明 $\text{[math]}$ 和 $\text{[math]}$ ，则这两个三角形全等的依据是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，若要证明 $\text{[math]}$ ≌ $\text{[math]}$ ，还需要补充一个条件，则正确的补充方法是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 用4个长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的长方形拼成如图所示的大正方形，则用这个图形可以验证的恒等式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、解答题

9. 观察下列关于自然数的等式：
3²﹣4×1=4+1    ①
5²﹣4×2=16+1   ②
7²﹣4×3=36+1   ③
…
根据上述规律解决下列问题：
（1）完成第四个等式；
（2）写出你猜想的第n个等式（用含n的式子表示），并验证其正确性．

查看解析收藏纠错

+选题
10. 老师在黑板上写了三个算式，希望同学们认真观察，发现规律.请你结合这些算式，解答下列问题：
请观察以下算式：

① $\text{[math]}$ ；

② $\text{[math]}$ ；

③ $\text{[math]}$ ；

……

试写出符合上述规律的第五个算式；

验证：设两个连续奇数为2n+1， $\text{[math]}$ (其中 $\text{[math]}$ 为正整数)，并说明它们的平方差是8的倍数；

查看解析收藏纠错

+选题
11. 观察下列关于自然数的等式：
2×4﹣1²+1=8
3×5﹣2²+1=12
4×6﹣3²+1=16
5×7﹣4²+1=20
…
利用等式的规律，解答下列问题：
（1）若等式8×10﹣a²+1=b（a，b都为自然数）具有以上规律，则a等于多少，a+b等于多少．
（2）写出第n个等式（用含n的代数式表示），并验证它的正确性．

查看解析收藏纠错

+选题
12. 发现：一个三位数的百位上数字为a，十位上数字为(a+1)，个位上数字为(a＋2)；把这个三位数的百位上数字与个位上的数字交换得到一个新三位数，新三位数与原三位数的差是9的倍数．
验证：

（1） ①765—567=9× ；

②通过列式计算，说明新三位数与原三位数的差是9的倍数；

（2）延伸：新三位数与原三位数的和是正整数m的倍数，则m=____________，并说明理由．

查看解析收藏纠错

+选题
13. 观察以下等式：
第1个等式： $\text{[math]}$ ，
第2个等式： $\text{[math]}$ ，
第3个等式： $\text{[math]}$ ，
……
按照以上规律，解决下列问题：

（1）写出第4个等式：；

（2）写出你猜想的第 $\text{[math]}$ 个等式（用含 $\text{[math]}$ 的式子表示），并验证当 $\text{[math]}$ 时，猜想成立．

查看解析收藏纠错

+选题
14. 已知x≠1．观察下列等式：
(1-x)(1+x)=1-x² ；

(1-x)(1+x+x²)=1-x³；

(1-x)(1+x+x²+x³)=1-x⁴；

（1）猜想： (1-x)(1+x+x²+x³+……+x^n-1)=；

（2）证明你在(1)中的猜想；

（3）根据你的猜想计算：(x-1)(x²⁰²³+x²⁰²²+x²⁰²¹+……+x²+x+1)．

查看解析收藏纠错

+选题
15. 实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b反射的光线为n．

（1）当 $\text{[math]}$ 时，若 $\text{[math]}$ ，则∠2＝，∠3＝；

（2）当 $\text{[math]}$ 时，若 $\text{[math]}$ ，则∠3＝；

（3）根据（1）（2）结果，反过来猜想：当两平面镜a，b的夹角∠3为多少度时， $\text{[math]}$ ．请说明理由（可以在图中添加适当的角度标记进行说明）

查看解析收藏纠错

+选题
16. 有三个多项式：① $\text{[math]}$ ，② $\text{[math]}$ ，③ $\text{[math]}$ ，请挑选其中两个多项式，满足所挑选的两个多项式的和是单项式，并加以验证（只要求写出一种正确的选法）.

（1）你挑选的两个多项式是；

（2）写出你的验证过程.

查看解析收藏纠错

+选题
17. 美国第二十任总统伽菲尔德的证法，被称为“总统证法”．如图，梯形由三个直角三角形组合而成，利用面积公式，验证勾股定理．

查看解析收藏纠错

+选题
18. 发现：五个连续的偶数中，存在前三个偶数的平方和等于后两个偶数的平方和．
验证：

（1） $\text{[math]}$

（2）若还存在五个连续的偶数，前三个偶数的平方和可以等于后两个偶数的平方和，设中间的偶数为n，求n

（3）延伸：是否存在三个连续的奇数中，有前两个奇数的平方和可以等于后一个奇数的平方，请说明理由．

查看解析收藏纠错

+选题
19. 观察：
$\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ =2 $\text{[math]}$ ，即 $\text{[math]}$ =2 $\text{[math]}$ ； $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ =3 $\text{[math]}$ ，即 $\text{[math]}$ =3 $\text{[math]}$ .猜想 $\text{[math]}$ 等于什么，并通过计算验证你的猜想.

查看解析收藏纠错

+选题
20. 阅读下列材料：
小铭和小雨在学习过程中有如下一段对话：

小铭：“我知道一般当m≠n时， $\text{[math]}$ ≠ $\text{[math]}$ .可是我见到有这样一个神奇的等式：

$\text{[math]}$ = $\text{[math]}$ （其中a ， b为任意实数，且b≠0）．你相信它成立吗？”

小雨：“我可以先给a ， b取几组特殊值验证一下看看．”

完成下列任务：

（1）请选择两组你喜欢的、合适的a ， b的值，分别代入阅读材料中的等式，写出代入后得到的具体等式并验证它们是否成立（在相应方框内打勾）；
① 当a=，b=时，等式（成立；不成立）；

② 当a=，b=时，等式（成立；不成立）．

（2）对于任意实数a ， b（b≠0），通过计算说明 $\text{[math]}$ = $\text{[math]}$ 是否成立．

查看解析收藏纠错

+选题
21. 发现任意三个连续的整数中，最大数与最小数这两个数的平方差是4的倍数；
验证：

（1） $\text{[math]}$ 的结果是4的几倍？

（2）设三个连续的整数中间的一个为n，计算最大数与最小数这两个数的平方差，并说明它是4的倍数；
延伸：说明任意三个连续的奇数中，最大的数与最小的数这两个数的平方差是8的倍数.

查看解析收藏纠错

+选题
22. 据说夏禹治水时，在黄河支流洛水中浮现出一只大乌龟，背上有一个很奇怪的图彤，古人认为是一种祥瑞，预示着洪水将被夏禹王彻底制服。后人称之为”洛书”，即现在的三阶幻方。三阶幻方，具有一个十分“漂亮”的性质：每一横行、每一竖列和对角线上的三个数的和都相等．不信，我们来验证一下．
一般地，一个n行n列的正方形方格中，每一横行、每一竖列和对角线上的数字和都相等，这样的数字方阵称为n阶幻方．

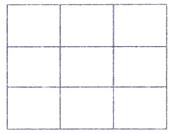
请将-2，-1，0，1，2，3，4，5，6填入到3×3的方格中，使得每行、每列、斜对角的三个数之和相等．

想一想：这9个数与原来9个数有什么关系?这9个数可以由原来9个数怎么变过来?

查看解析收藏纠错

+选题

2023-2024学年北师大版数学八年级上册7.1为什么要证明 同步练习（基础卷）

一、单选题

二、解答题

相关试卷 收起∨

2023-2024学年北师大版数学八年级上册7.1为什么要证明同步练习（基础卷）

相关试卷收起∨