浙教版备考2023年中考数学一轮复习9.探索图形规律

修改时间：2022-11-28 浏览次数：61 类型：一轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题（每题3分，共30分）

1. 如图，正方形的周长为8个单位，在该正方形的4个顶点处分别标上0，2，4，6，先让正方形上表示数字6的点与数轴上表﹣3的点重合，再将数轴按顺时针方向环绕在该正方形上，则数轴上表示2017的点与正方形上的数字对应的是（）

A . 0 B . 2 C . 4 D . 6

查看解析收藏纠错

+选题
2. 如图，在纸面所在的平面内，一只电子蚂蚁从数轴上表示原点的位置O点出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其移动路线如图所示，第1次移动到A₁ ，第2次移动到A₂ ，第3次移动到A₃ ， ……，第n次移动到A_n ，则△OA₂A₂₀₂₂的面积是（）

A . 505 B . $\text{[math]}$ C . $\text{[math]}$ D . 1011

查看解析收藏纠错

+选题
3. 下列图形都是用同样大小的★按一定规律组成的，其中第①个图形中共有5个★，第②个图形中共有11个★，…，则第⑩个图形中★的个数为（）

A . 109 B . 111 C . 131 D . 157

查看解析收藏纠错

+选题
4. 如图，在△ABC中， $\text{[math]}$ ， $\text{[math]}$ 的平分线与 $\text{[math]}$ 的平分线交于点 $\text{[math]}$ ，得 $\text{[math]}$ ， $\text{[math]}$ 的平分线与 $\text{[math]}$ 的平分线交于点 $\text{[math]}$ ，得 $\text{[math]}$ ， …， $\text{[math]}$ 的平分线与 $\text{[math]}$ 的平分线交于点 $\text{[math]}$ ，得 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图，正方形 $\text{[math]}$ 边长为1，以 $\text{[math]}$ 为边作第2个正方形 $\text{[math]}$ ，再以 $\text{[math]}$ 为边作第3个正方形 $\text{[math]}$ ， ……，按照这样的规律作下去，第2022个正方形的边长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，在平面直角坐标系中，半径均为2个单位长度的半圆组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒π个单位长度，则第2023秒时，点P的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，在平面直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ； $\text{[math]}$ ；按此做法进行下去，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 图1是第七届国际数学教育大会（ICME.7）的会徽，主体图案是由图2的一连串直角三角形演化而成，其中OA₁＝A₁A₂＝A₂A₃＝……＝A_n_﹣₁A_n＝1，若OA₅⋅OA_n的值是整数，且1≤n≤50，则符合条件的n有（）

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
9. 观察并找出图形变化的规律，则第2021个图形中黑色正方形的数量是（）

A . 2020 B . 3031 C . 2021 D . 3032

查看解析收藏纠错

+选题
10. 如图，在平面直角坐标系上有点 $\text{[math]}$ ，点 $\text{[math]}$ 第一次跳动至点 $\text{[math]}$ ，第二次点 $\text{[math]}$ 跳动至点 $\text{[math]}$ ，第三次点 $\text{[math]}$ 跳动至点 $\text{[math]}$ ，第四次点 $\text{[math]}$ 跳动至点 $\text{[math]}$ ， $\text{[math]}$ ，依此规律跳动下去，则点 $\text{[math]}$ 与点 $\text{[math]}$ 之间的距离是（）

A . 2021 B . 2020 C . 2019 D . 2018

查看解析收藏纠错

+选题

二、填空题（每题3分，共18分）

11. 图1是一个三角形，分别连接这个三角形三边的中点得到图2；再分别连接图2中间小角形三边的中点，得到图3，按上面的方法继续下去.则图2中共有个三角形，第n个图形（图1是第一个图形）中共有个三角形（用含n的代数式表示）.

查看解析收藏纠错

+选题
12. 圆上有五个点，这五个点将圆分成五等份（每一份称为一段弧长），把这五个点按顺时针方向依次编号为1，2，3，4，5，若从某一点开始，沿圆周顺时针方向行走，点的编号是数字几，就走几段弧长，则称这种走法为一次“移位”．如：小明在编号为3的点，那么他应走3段弧长，即从3→ 4→5→1为第一次“移位”，这时他到达编号为1的点，然后从1→2为第二次“移位”．若小明从编号为4的点开始，第2014次“移位”后，他到达编号为的点．

查看解析收藏纠错

+选题
13. 图中所示的为“毕达哥拉斯树”的“生长”过程．如图①，一个边长为a的正方形，经过第一次“生长”后在它的上侧长出两个小正方形，且三个正方形所围成的三角形是直角三角形；再经过一次“生长”后变成了图②；如此继续“生长”下去，则第2000次“生长”后，这棵“毕达哥拉斯树”上所有正方形的面积和为．

查看解析收藏纠错

+选题
14. 如图是用棋子摆成的“上”字：如果按照以下规律继续摆下去，第n个“上”字需用枚棋子．

查看解析收藏纠错

+选题
15. 下面是小朋友用火柴棒拼出的一系列图形，仔细观察，找出规律，并解答下列问题：
第n个图形共有根火柴棒．

查看解析收藏纠错

+选题
16. 如图， $\text{[math]}$ 是边长为1的等边三角形，分别取 $\text{[math]}$ 边的中点D、E，连接 $\text{[math]}$ ，作 $\text{[math]}$ 得到四边形 $\text{[math]}$ ，它的周长记作 $\text{[math]}$ ；分别取 $\text{[math]}$ 的中点 $\text{[math]}$ ，连接 $\text{[math]}$ ，作 $\text{[math]}$ ，得到四边形 $\text{[math]}$ ，它的周长记作 $\text{[math]}$ ， …，照此规律作下去，则 $\text{[math]}$ 等于．

查看解析收藏纠错

+选题

三、解答题（共10题，共72分）

17. 完成下列填空：

（1）已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，依据上述规律，则 $\text{[math]}$ =.

（2）有若干张边长都是2的四边形纸片和三角形纸片，从中取一些纸片按如图所示的顺序拼接起来 $\text{[math]}$ 排在第一位的是四边形 $\text{[math]}$ ，可以组成一个大的平行四边形或一个大的梯形.如果所取的四边形与三角形纸片数的和是5时，那么组成的大平行四边形或梯形的周长是；如果所取的四边形与三角形纸片数的和是 $\text{[math]}$ ，那么组成的大平行四边形或梯形的周长是.

（3）下面是按一定规律排列的一列数：
第1个数： $\text{[math]}$ ；

第2个数： $\text{[math]}$ ；

第3个数： $\text{[math]}$ ； $\text{[math]}$

则第 $\text{[math]}$ 个数为：.

查看解析收藏纠错

+选题
18. 如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的，若将露出的表面都涂上颜色（底面不涂色），观察该图，探究其中的规律．

（1）第1个几何体中只有2个面涂色的小立方体共有个；第2个几何体中只有2个面涂色的小立方体共有个；第3个几何体中只有2个面涂色的小立方体共有个．

（2）求出第10个几何体中只有2个面涂色的小立方体的块数．

（3）求出前100个几何体中只有2个面涂色的小立方体的块数的和．

查看解析收藏纠错

+选题
19. 如图，平面内有公共端点的六条射线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，从射线 $\text{[math]}$ 开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，…．

（1） “25”在射线上；

（2）请用含 $\text{[math]}$ ( $\text{[math]}$ 为自然数)的代数式表示射线OA、OC、OE上数字的排列规律；

（3） “2009”在哪条射线上？

查看解析收藏纠错

+选题
20. 实际问题：
婚礼上有116名宾客，地面上水平放置了一个长方体蛋糕，要保证这116名宾客都能分得蛋糕（忽略大小，水平切割的方向只能与地面平行，垂直切割只能与地面垂直），小明说我10刀即可完成任务，你认为小明是怎样切这个蛋糕才能完成任务．
问题探究：
为解决这个问题我们从最简单的长方形分割开始研究．
探究一：用一条直线分一个长方形，最多可以分成几部分？
如图1所示，一条线来分多出1部分，最多分成1+1=2部分；
探究二：用2条直线分一个长方形，最多可以分成几部分？
如图2所示，第2条线与第一条线相交，多出2部分，最多分成1+1+2=4部分；
探究三：用3条直线分一个长方形，最多可以分成几部分？
如图3所示，第3条线与前2条线相交，多出3部分，最多分成1+1+2+3=7部分；
探究四：用4条直线分一个长方形，最多可以分成几部分？
如图4所示，第4条线与原来3条线相交，多出4部分，最多分1+1+2+3+4=11部分；

（1）探究五：用5条直线分一个长方形，第5条线与原来4条线相交，多出部分，即最多分成部分；

（2）探究六：用 $\text{[math]}$ 条直线分一个长方形，最多可以分成部分；（用含 $\text{[math]}$ 的代数式表示）

（3）探究七：我们可以将开始提出的问题转化为切割长方体，借助以上探究长方形切割的结论如何将长方体切割成14块？
我们只需要在探究三的基础上，先在长方体中竖直切割3刀最多分成7块，平行于地面切一刀，此时4刀可切成7×2=14块．
探究八：如何用最少的切割次数，将一个长方体蛋糕切割成44块，请说明切割过程，无需画图；
问题解决：

（4）婚礼上有116名宾客，地面上放了一个长方体蛋糕，要保证这116名宾客都能分得蛋糕（忽略大小，水平切割的方向只能与地面平行，垂直切割只能与地面垂直），小明说我10刀即可完成任务，你认为小明是怎样切这个蛋糕？请说明切割的过程，无需画图．

查看解析收藏纠错

+选题
21. 在3×3的方格中，每行、每列及对角线上的3个代数式的和都相等，我们把这样的方格图叫做“等和格”. 如图1的“等和格”中，每行、每列及对角线上的3个代数式的和都等于15.

（1）在图2的“等和格”方格图中，可得a＝.（用含b的代数式表示）；

（2）在图3的“等和格”方格图中，可得a＝，b＝；

（3）在图4的“等和格”方格图中，可得b＝.

查看解析收藏纠错

+选题
22. 图1中，有一个平行四边形；
图2中，由2个相同的平行四边形拼成一排的图形，这图形中可以找到3个平行四边形；
图3中，由3个相同的平行四边形拼成一排的图形，这图形中可以找到6个平行四边形；
由此我们可以提出一个这样的问题：
图4中，由4个相同的平行四边形拼成一排的图形中，可以找到几个平行四边形？
答：10个
请你根据以上事实，将一些相同的平行四边形横向或纵向拼接，由此提出一个数学问题，并写出答案．

查看解析收藏纠错

+选题
23. 在同一平面内有n条直线，当n＝1时，如图①，一条直线将一个平面分成两个部分；当n＝2时，如图②，两条直线将一个平面最多分成四个部分.

（1）在作图区分别画出当n＝3时，三条直线将一个平面分成最少部分和最多部分的情况；

（2）当n＝4时，请写出四条直线将一个平面分成最少部分的个数和最多部分的个数；

（3）若n条直线将一个平面最多分成a_n个部分，（n＋1）条直线将一个平面最多分成a_n＋1个部分，请写出a_n ， a_n＋1 ， n之间的关系式.

查看解析收藏纠错

+选题
24. 如图

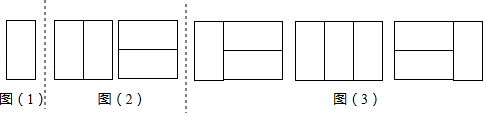
（问题）用n个2×1矩形，镶嵌一个2×n矩形，有多少种不同的镶嵌方案？（2×n矩形表示矩形的邻边是2和n）

（探究）不妨假设有a_n种不同的镶嵌方案．为探究a_n的变化规律，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进，最后猜想得出结论．

探究一：用1个2×1矩形，镶嵌一个2×1矩形，有多少种不同的镶嵌方案？

如图（1），显然只有1种镶嵌方案．所以，a₁＝1．

探究二：用2个2×1矩形，镶嵌一个2×2矩形，有多少种不同的镶嵌方案？

如图（2），显然只有2种镶嵌方案．所以，a₂＝2．

探究三：用3个2×1矩形，镶嵌一个2×3矩形，有多少种不同的镶嵌方案？

一类：在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形，有1种镶嵌方案；

二类：在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形，有2种镶嵌方案；

如图（3）．所以，a₃＝1+2＝3．

（1）探究四：用4个2×1矩形，镶嵌一个2×4矩形，有多少种不同的镶嵌方案？
一类：在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形，有种镶嵌方案；

二类：在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形，有种镶嵌方案；

所以，a₄＝．

（2）探究五：用5个2×1矩形，镶嵌一个2×5矩形，有多少种不同的镶嵌方案？
（仿照上述方法，写出探究过程，不用画图）

……

（结论）用n个2×1矩形，镶嵌一个2×n矩形，有多少种不同的镶嵌方案？

（直接写出a_n与a_n_﹣1 ， a_n_﹣2的关系式，不写解答过程）．

（应用）用10个2×1矩形，镶嵌一个2×10矩形，有 ▲ 种不同的镶嵌方案．

查看解析收藏纠错

+选题
25. 如图所示，由一些点组成形如三角形的图形，每条“边”（包括两个顶点）有 $\text{[math]}$ 个点，每个图形的总点数记为S ．

（1）当 $\text{[math]}$ 时，S的值为；当 $\text{[math]}$ 时，S的值为；

（2）每条“边”有n个点时的总点数S是（用含n的式子表示）；

（3）当 $\text{[math]}$ 时，总点数S是多少？

查看解析收藏纠错

+选题
26. 定义：按螺旋式分别延长n边形的n条边至一点，若顺次连接这些点所得的图形与原多边形相似，则称它为原图形的螺旋相似图形.例如：如图1，分别延长多边形A₁A₂…A_n的边得A₁′，A₂′，…，A_n′，若多边形A₁′A₂′…A_n′与多边形A₁A₂…An相似，则多边形A₁′A₂′…A_n′就是A₁A₂…A_n的螺旋相似图形.

（1）如图2，已知△ABC是等边三角形，作出△ABC的一个螺旋相似图形，简述作法，并给以证明.

（2）如图3，已知矩形ABCD，请探索矩形ABCD是否存在螺旋相似图形，若存在，求出此时AB与BC的比值；若不存在，说明理由.

（3）如图4，△ABC是等腰直角三角形，AC＝BC＝2，分别延长CA，AB，BC至A′，B′，C′，使△A′B′C′是△ABC的螺旋相似三角形.若AA′＝kAC，请直接写出BB′，CC′的长（用含k的代数式表示）

查看解析收藏纠错

+选题

浙教版备考2023年中考数学一轮复习9.探索图形规律

一、单选题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共10题，共72分）

相关试卷 收起∨

相关试卷收起∨