题型:实践探究题 题类:模拟题 难易度:困难
2017年山东省青岛市市北区中考数学一模试卷
探究题
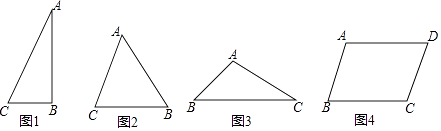
【问题提出】
已知任意三角形的两边及夹角(是锐角),求三角形的面积.
【问题探究】
为了解决上述问题,让我们从特殊到一般展开探究.
探究:在Rt△ABC(图1)中,∠ABC=90°,AC=b,BC=a,∠C=α,求△ABC的面积(用含a、b、α的代数式表示)
在Rt△ABC中,∠ABC=90°
∴sinα=
∴AB=b•sinα
∴S△ABC= BC•AB=
absinα
锐角△ABC(图2)中,AC=b,BC=a,∠C=α(0°<α<90°)
求:△ABC的面积.(用含a、b、α的代数式表示)
钝角△ABC(图3)中,AC=b,BC=a,∠C=α(0°<α<90°)
求:△ABC的面积.(用含a、b、α的代数式表示)
用文字叙述:已知任意三角形的两边及夹角(是锐角),求三角形面积的方法
是
求:平行四边形ABCD的面积.(用含a、b、α的代数式表示)
试题篮