试题 试卷
题型：单选题 题类：真题 难易度：普通
2017年重庆市中考数学试卷（b卷）
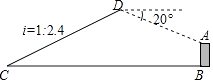
如图，已知点C与某建筑物底端B相距306米（点C与点B在同一水平面上），某同学从点C出发，沿同一剖面的斜坡CD行走195米至坡顶D处，斜坡CD的坡度（或坡比）i=1：2.4，在D处测得该建筑物顶端A的俯视角为20°，则建筑物AB的高度约为（精确到0.1米，参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364）（ ）
已知：如图①、②，解答下面各题：
（1）图①中，∠AOB=55°，点P在∠AOB内部，过点P作PE⊥OA，PF⊥OB，垂足分别为E、F，求∠EPF的度数．
（2）图②中，点P在∠AOB外部，过点P作PE⊥OA，PF⊥OB，垂足分别为E、F，那么∠P与∠O有什么关系？为什么？
（3）通过上面这两道题，你能说出如果一个角的两边分别垂直于另一个角的两边，则这两个角是什么关系？
（4）如果一个角的两边分别平行于另一个角的两边，则这两个角是什么关系？（请画图说明结果，不需要过程）
试题篮
