如图，装修工人向墙上钉木条.若∠2＝110°，要使木条b与a平行，则∠1的度数等于(      ).

如图，下列条件：①∠1=∠2；②∠A=∠4；③∠1=∠4；④∠A+∠3=180°；⑤∠C=∠BDE，其中能判定AB∥DF的有（　　）

填写下列解题过程中的推理根据：

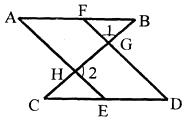
已知：如图，点F、E分别在AB、CD上，AE、DF分别与BC相交于H、G，∠A＝∠D，∠1＋∠2＝180°.说明：AB∥CD

解：∵∠1＝∠CGD（{#blank#}1{#/blank#}）

    ∠1＋∠2＝180°

∴{#blank#}2{#/blank#}.

    ∴AE//FD （{#blank#}3{#/blank#}）

    ∴{#blank#}4{#/blank#}（两直线平行，同位角相等）

    又∠A＝∠D

    ∴∠D＝∠BFD

∴{#blank#}5{#/blank#}（{#blank#}6{#/blank#}）

（Ⅰ）尺规作图：

（i）在AN上取一点C，使BC＝BA；

（ii）作∠MBC的平分线BD，（保留作图痕迹，不写作法）

（Ⅱ）在（Ⅰ）的条件下，求证：BD∥AN．