初中数学浙教版八年级下学期期末复习专题13 矩形的性质与判定

1. 数学课上，老师要同学们判断一个四边形门框是否为矩形．下面是某合作小组4位同学拟定的方案，其中正确的是（）

A . 测量对角线是否互相平分 B . 测量两组对边是否分别相等 C . 测量一组对角是否都为直角 D . 测量三个角是否为直角

查看解析收藏纠错

+选题
2. 如图，在 $\text{[math]}$ ABCD中，对角线AC、BD相交于点O，OA=3cm，若要使平行四边形ABCD为矩形，则OB的长度为（）

A . 4cm B . 3cm C . 2cm D . 1cm

查看解析收藏纠错

+选题
3. 如图，小明将一张长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的长方形纸 $\text{[math]}$ 剪去了一角，量得 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图，矩形ABCD中，对角线AC、BD相交于点O，过点O作OE⊥BD交AD于点E，已知AB=2， $\text{[math]}$ ，则AE的长为（）

A . 1.5 B . 2 C . 2.5 D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图，长方形ABCD是由6个正方形组成，其中有两个一样大的正方形，且最小正方形边长为1，则长方形ABCD的边长DC为（）

A . 10 B . 13 C . 16 D . 19

查看解析收藏纠错

+选题
6. 矩形 $\text{[math]}$ 的两条对角线相交于O点， $\text{[math]}$ ，若 $\text{[math]}$ ，则矩形的对角线 $\text{[math]}$ 的长为（）

A . 2 B . 4 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图， $\text{[math]}$ 的对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点O，添加下列条件后，不能得出四边形 $\text{[math]}$ 是矩形的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 下列命题中，能判断四边形是矩形的是（）

A . 对角线相等 B . 对角线互相平分 C . 对角线相等且互相平分 D . 对角线互相垂直

查看解析收藏纠错

+选题
9. 在▱ABCD中，对角线AC、BD相交于点O，若∠ABC＝90°，则下列结论错误的是（）

A . AC＝BD B . OA＝OB C . AC⊥BD D . AB＝CD

查看解析收藏纠错

+选题
10. 如图△ABC中，AC的垂直平分线分别交AC，AB于点D，F，BE⊥DF交DF的延长线于点E，已知∠A=30°，BC=2，AF=BF，则四边形BCDE的面积是（）

A . 2 $\text{[math]}$ B . 3 $\text{[math]}$ C . 4 D . 4 $\text{[math]}$

查看解析收藏纠错

+选题

11. 在矩形ABCD中，AC与BD相交于点O，若OA＝2，则BD的长是.

查看解析收藏纠错

+选题
12. 如图，四边形 $\text{[math]}$ 的对角线互相平分，请你添加一个条件，使它成为矩形，你添加的条件是．

查看解析收藏纠错

+选题
13. 长方形的宽为 $\text{[math]}$ ，面积为6，则长方形的长为 .

查看解析收藏纠错

+选题
14. 矩形的一个角的平分线分一边为2和4两部分，则这个矩形的对角线的长．

查看解析收藏纠错

+选题
15. 如图，点E、F、G、H分别是矩形ABCD边AB、BC、CD、DA上的点，且HG与EF交于点I，连接HE、FG，若AB=6，BC=5，EF//AD，HG//AB，则HE+FG的最小值是．

查看解析收藏纠错

+选题
16. 如图，在矩形ABCD中，BC＝40cm，点P和点Q分别从点B和点D出发，按逆时针方向沿矩形ABCD的边运动，点P和点Q的速度分别为3cm/s和1cm/s，则最快s后，四边ABPQ成为矩形.

查看解析收藏纠错

+选题

17. 如图，延长矩形 $\text{[math]}$ 的边 $\text{[math]}$ 至点E，使 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ 平分 $\text{[math]}$ ．

查看解析收藏纠错

+选题
18. 如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．

求证：四边形AEBD是矩形．

查看解析收藏纠错

+选题
19. 已知：如图，∠MAN＝90°，线段a和线段b
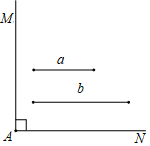
求作：矩形ABCD，使得矩形ABCD的两条边长分别等于线段a和线段b．

下面是小东设计的尺规作图过程．

作法：如图，

①以点A为圆心，b为半径作弧，交AN于点B；

②以点A为圆心，a为半径作弧，交AM于点D；

③分别以点B、点D为圆心，a、b长为半径作弧，两弧交于∠MAN内部的点C；

④分别连接BC，DC．

所以四边形ABCD就是所求作的矩形．

根据小东设计的尺规作图过程，

（1）使用直尺和圆规，补全图形；（保留作图痕迹）

（2）完成下面的证明．
证明：

∵AB＝；AD＝；

∴四边形ABCD是平行四边形．

∵∠MAN＝90°；

∴四边形ABCD是矩形（填依据）．

查看解析收藏纠错

+选题
20. 如图所示，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F，连结AE、CF.

（1）求证：AF＝CE；

（2）若AC＝EF，试判断四边形AFCE是什么样的四边形，并证明你的结论．

查看解析收藏纠错

+选题
21. 如图，在▱ABCD中，AC＝8，BD＝12，点E、F在对角线BD上，点E从点B出发以1个单位每秒的速度向点D运动，同时点F从点D出发以相同速度向点B运动，到端点时运动停止，运动时间为t秒．

（1）求证：四边形AECF为平行四边形．

（2）求t为何值时，四边形AECF为矩形．

查看解析收藏纠错

+选题
22. 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 于点 $\text{[math]}$ ，延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

（1）求证：四边形 $\text{[math]}$ 是矩形；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
23. 如图，在 $\text{[math]}$ 中，点O是 $\text{[math]}$ 边上的一个动点，过点O作直线 $\text{[math]}$ ， $\text{[math]}$ 以及外角 $\text{[math]}$ 的平分线分别交 $\text{[math]}$ 于点E、F.

（1）求证： $\text{[math]}$ ；

（2）当点O运动到 $\text{[math]}$ 边的什么位置时，四边形 $\text{[math]}$ 是矩形？回答并证明你的结论.

查看解析收藏纠错

+选题
24. 在四边形ABCD中，∠A=∠B=∠C=∠D=90°，AB=CD=10，BC=AD=6，P为射线BC上一点，将△ABP沿直线AP翻折至△AEP的位置，使点B落在点E处.

（1）若P为BC上一点
a：如图1，当点E落在边CD上时，直接写出此时CE=.

b：如图2，连接CE，若CE $\text{[math]}$ AP，则BP与BC有何数量关系？请说明理由.

（2）如图3，如果点P在BC的延长线上时，当△PEC为直角三角形时，求PB的长.

查看解析收藏纠错

+选题

初中数学浙教版八年级下学期期末复习专题13 矩形的性质与判定

一、单选题

二、填空题

三、解答题

相关试卷收起∨

初中数学浙教版八年级下学期期末复习专题13 矩形的性质与判定

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨