河南省洛阳市汝阳县2021年数学中考一模试卷

1. 抛物线y＝（x﹣2）²+3的对称轴是（）

A . 直线x＝﹣3 B . 直线x＝3 C . 直线x＝2 D . 直线x＝﹣2

查看解析收藏纠错

+选题
2. 为了解汝阳县汽车站今年春节期间每天乘车人数这个问题，随机抽查了其中七天的乘车人数，被抽查的这七天的乘车人数是这个问题的（）.

A . 总体 B . 个体 C . 样本 D . 以上都不对

查看解析收藏纠错

+选题
3. 如图，被阴影覆盖的可能是下面哪一个数（）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 以上都不对

查看解析收藏纠错

+选题
4. 关于x的一元二次方程x²+4x+k＝0有两个相等的实数根，则k的值为（）

A . k＝4 B . k＝﹣4 C . k≥﹣4 D . k≥4

查看解析收藏纠错

+选题
5. 李红同学遇到了这样一道题： $\text{[math]}$ tan(α+20°)=1，你猜想锐角α的度数应是（）

A . 40° B . 30° C . 20° D . 10°

查看解析收藏纠错

+选题
6. 若AB是⊙O的直径，∠ACB＝90°，则点C一定在（）

A . ⊙O内 B . ⊙O外 C . ⊙O上 D . ⊙O内或⊙O上

查看解析收藏纠错

+选题
7. 已知二次函数y=ax²+bx+c，且a＜0，a-b+c＞0，则一定有（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 某市公园的东、西、南、北方向上各有一个入口，周末佳佳和琪琪随机从一个入口进入该公园游玩，则佳佳和琪琪恰好从同一个入口进入该公园的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，已知⊙O中∠AOB度数为100°，C是圆周上的一点，则∠ACB的度数为（）

A . 130° B . 100° C . 80° D . 50°

查看解析收藏纠错

+选题
10. 已知二次函数y=ax²+bx+c的图象如图所示，有以下结论：
①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④9a﹣3b+c＜0；⑤c﹣a＞1.其中所有正确结论的序号是(　　)

A . ①② B . ①③④ C . ①②③④ D . ①②③④⑤

查看解析收藏纠错

+选题

11. 圆锥的底面半径为5cm，圆锥母线长为13cm，则圆锥的侧面积为cm²（结果保留π）.

查看解析收藏纠错

+选题
12. 一个不透明的盒子里有红色、黄色、白色小球共80个.它们除颜色外均相同，小文将这些小球摇匀后从中随机摸出一个记下颜色，再把它放回盒中，不断重复，多次试验后他发现摸到红色、黄色小球的频率依次为30%和40%.由此可估计盒中大约有白球个.

查看解析收藏纠错

+选题
13. 如图，在⊙E中，弦AB与CD相交于坐标原点O，已知B（0，﹣3），C（﹣2，0），D（6，0），则点A的坐标是.

查看解析收藏纠错

+选题
14. 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 是线段 $\text{[math]}$ 上的一个动点，则 $\text{[math]}$ 的最小值是.

查看解析收藏纠错

+选题

15. 已知实数a是一元二次方程x²－2016x＋1＝0的根，求代数式a²－2015a－ $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
16. 先化简，再求代数式 $\text{[math]}$ ÷（a﹣1﹣ $\text{[math]}$ ）的值，其中a＝2sin60°﹣2tan45°.

查看解析收藏纠错

+选题
17. 如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD于点E，DA平分∠BDE．

（1）求证：AE是⊙O的切线；

（2）如果AB=4，AE=2，求⊙O的半径．

查看解析收藏纠错

+选题
18. 已知m，n是方程x²﹣2x﹣1＝0的两个根，是否存在实数a使﹣（m+n）（7m²﹣14m+a）（3n²﹣6n﹣7）的值等于8？若存在，求出a的值；若不存在，请说明理由.

查看解析收藏纠错

+选题

19. 某校为了解学生对“防溺水”安全知识的掌握情况，从全校1500名学生中随机抽取部分学生进行测试，并将测试成绩（百分制，得分均为整数）进行统计分析，绘制了不完整的频数表和频数直方图.

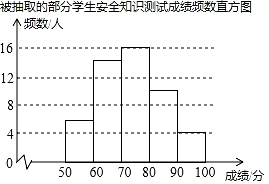
组别	成绩x（分）	频数（人）	频率
A组	50≤x＜60	6	0.12
B组	60≤x＜70	a	0.28
C组	70≤x＜80	16	0.32
D组	80≤x＜90	10	0.20
E组	90≤x≤100	4	0.08

由图表中给出的信息回答下列问题：

（1）表中的a＝；抽取部分学生的成绩的中位数在组；

（2）把如图的频数直方图补充完整；

（3）如果成绩达到80分以上（包括80分）为优秀，请估计该校1500名学生中成绩优秀的人数.

查看解析收藏纠错

+选题

20. 某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系)．
根据图象提供的信息，解答下列问题：

（1）由已知图象上的三点坐标，求累积利润s(万元)与时间t(月)之间的函数关系式；

（2）求截止到几月末公司累积利润可达到30万元；

（3）求第8个月公司所获利润为多少万元?

查看解析收藏纠错

+选题
21. 如图1是一种手机平板支架，由托板、支撑板和底座构成，手机放置在托板上，图2是其侧面结构示意图，量得托板长 $\text{[math]}$ ，支撑板长 $\text{[math]}$ ，底座长 $\text{[math]}$ ，托板 $\text{[math]}$ 固定在支撑板顶端点C处，且 $\text{[math]}$ ，托板 $\text{[math]}$ 可绕点 $\text{[math]}$ 转动，支撑板 $\text{[math]}$ 可绕点D转动．（结果保留小数点后一位）

（1）若 $\text{[math]}$ ， $\text{[math]}$ ，求点A到直线 $\text{[math]}$ 的距离；

（2）为了观看舒适，在（1）的情况下，把 $\text{[math]}$ 绕点C逆时针旋转 $\text{[math]}$ 后，再将 $\text{[math]}$ 绕点D顺时针旋转，使点B落在直线 $\text{[math]}$ 上即可，求 $\text{[math]}$ 旋转的角度．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
22. 已知二次函数y₁=a（x﹣2）²+k中，函数y₁与自变量x的部分对应值如表：
x
…
1
2
3
4
…
y
…
2
1
2
5
…

（1）求该二次函数的表达式；

（2）将该函数的图象向左平移2个单位长度，得到二次函数y₂的图象，分别在y₁、y₂的图象上取点A（m，n₁）B（m+1，n₂），试比较n₁与n₂的大小．

查看解析收藏纠错

+选题
23. 如图

（问题探究）

已知：如图①所示，∠MPN的顶点为P，⊙O的圆心O从顶点P出发，沿着PN方向平移.

（1）如图②所示，当⊙O分别与射线PM，PN相交于A、B、C、D四个点，连接AC、BD，可以证得△PAC∽△，从而可以得到：PA•PB＝PC•PD.

（2）如图③所示，当⊙O与射线PM相切于点A，与射线PN相交于C、D两个点.求证：PA²＝PC•PD.

（3）（简单应用）
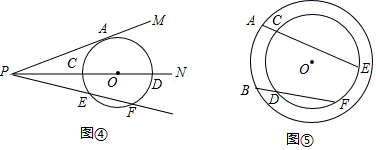
如图④所示，（2）中条件不变，经过点P的另一条射线与⊙O相交于E、F两点.利用上述（1），（2）两问的结论，直接写出线段PA与PE、PF之间的数量关系；当PA＝4 $\text{[math]}$ ，EF＝2，则PE＝.

（4）（拓展延伸）
如图⑤所示，在以O为圆心的两个同心圆中，A、B是大⊙O上的任意两点，经过A、B两点作线段，分别交小⊙O于C、E、D、F四个点.求证：AC•AE＝BD•BF.（友情提醒：可直接运用本题上面所得到的相关结论）

查看解析收藏纠错

+选题

河南省洛阳市汝阳县2021年数学中考一模试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

x	…	1	2	3	4	…
y	…	2	1	2	5	…

河南省洛阳市汝阳县2021年数学中考一模试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨