湘教版备考2021年中考数学二轮复习专题17一次函数

1. 某班“数学兴趣小组”探究出了有关函数 $\text{[math]}$ （图象如图）的三个结论：①方程 $\text{[math]}$ 有1个实数根，该方程的根是 $\text{[math]}$ ；②如果方程 $\text{[math]}$ 只有一个实数根，则a的取值范围是 $\text{[math]}$ 或 $\text{[math]}$ ；③如果方程 $\text{[math]}$ 有2个实数根，则a的取值范围是 $\text{[math]}$ 或 $\text{[math]}$ .你认为正确的结论个数有（）

A . 3 B . 2 C . 1 D . 0

查看解析收藏纠错

+选题
2. 甲，乙两车分别从A， B两地同时出发，相向而行.乙车出发2h后休息，当两车相遇时，两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h)，甲，乙两车到B地的距离分别为y₁(km)， y₂(km)， y₁ ， y₂关于x的函数图象如图.下列结论：①甲车的速度是 $\text{[math]}$ km/h；②乙车休息了0.5h；③两车相距a km时，甲车行驶了 $\text{[math]}$ h.正确的是（）

A . ①② B . ①③ C . ②③ D . ①②③

查看解析收藏纠错

+选题
3. 港口 $\text{[math]}$ 依次在同一条直线上，甲、乙两艘船同时分别从 $\text{[math]}$ 两港出发，匀速驶向 $\text{[math]}$ 港，甲、乙两船与 $\text{[math]}$ 港的距离 $\text{[math]}$ （海里）与行驶时间 $\text{[math]}$ （小时）之间的函数关系如图所示，则下列说法正确的有（）
① $\text{[math]}$ 两港之间的距离为60海里

②甲、乙两船在途中只相遇了一次

③甲船平均速度比乙船平均速度快30海里/时

④甲船到达 $\text{[math]}$ 港时，乙船还需要一个小时才到达 $\text{[math]}$ 港

⑤点 $\text{[math]}$ 的坐标为 $\text{[math]}$

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
4. 若点 $\text{[math]}$ 、 $\text{[math]}$ 是一次函数 $\text{[math]}$ 图象上不同的两点，记 $\text{[math]}$ ，当 $\text{[math]}$ 时，a的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图，四边形ABCD的顶点坐标分别为4（-4，0），B（-2，-1），C（3，0），D（0，3），当过点B的直线l将四边形ABCD分成面积相等的两部分时，直线I所表示的函数表达式为（）

A . y= $\text{[math]}$ B . y= $\text{[math]}$ C . y=x+1 D . y= $\text{[math]}$

查看解析收藏纠错

+选题
6. 将 $\text{[math]}$ 的正方形网格如图所示的放置在平面直角坐标系中，每个小正方形的顶点称为格点，每个小正方形的边长都是 $\text{[math]}$ ，正方形 $\text{[math]}$ 的顶点都在格点上，若直线 $\text{[math]}$ $\text{[math]}$ 与正方形 $\text{[math]}$ 有公共点，则 $\text{[math]}$ 的值不可能是（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 平面直角坐标系中，过点（-2，3）的直线经过一、二、三象限，若点（0，a），（-1，b），（c，-1）都在直线上，则下列判断正确的是（）

A . a＜b B . a＜3 C . b＜3 D . c＜-2

查看解析收藏纠错

+选题
8. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示.则下列结论：①A，B两城相距300千米；②乙车比甲车晚出发1小时，却早到1.5小时；③乙车出发后2.5小时追上甲车；④当甲、乙两车相距40千米时，t＝ $\text{[math]}$ 或t＝ $\text{[math]}$ ，其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
9. 如图①，一个立方体铁块放置在圆柱形水槽内，现以每秒固定的流量往水槽中注水，28秒时注满水槽，水槽内水面的高度y（厘米）与注水时间x（秒）之间的函数图象如图②所示，则圆柱形水槽的容积（在没放铁块的情况下）是（）

A . 8000cm³ B . 10000 cm³ C . 2000πcm³ D . 3000πcm³

查看解析收藏纠错

+选题
10. 如图，正方形 $\text{[math]}$ 的边长为4．点E，F，G，H分别在边 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上（编点除外），且 $\text{[math]}$ ．分别将 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 沿 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 翻折，得到四边形 $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ 则y关于x的函数图象大致为（）

A . B . C . D .

查看解析收藏纠错

+选题

11. 2020年1月15日上午八点，重庆马拉松赛在南滨路鸣枪起跑.为庆祝重马十周年，小明和小红约定一起参加迷你马拉松跑（全长5000 米）.比赛开始前，两人约定，完成总路程的 $\text{[math]}$ 时，速度快的人要在原地停留等待对方.比赛正式开始后，两人均匀速向前.已知小明率先完成全程的 $\text{[math]}$ ，并立刻停下，待小红追上时再次以原速匀速出发.一段时间后，小明体力不支，降速为原来的 $\text{[math]}$ 后匀速前进，最后同时与小红到达终点. 在此过程中，小红速度保持不变.如图是小明和小红之间的距离y（米）与两人出发的时间x（分钟）之间的函数图象.则小明开始降速时，小明距离终点还有米.

查看解析收藏纠错

+选题
12. 在一条公路上每隔100千米有一个仓库（如图），共有4个仓库．A仓库存有15吨货物，B仓库存有20吨货物，D仓库存有30吨货物，C仓库是空的．现在想把所有的货物集中存放在一个仓库里，如果每吨货物运输1千米需要0.5元的运费，那么最少要花元运费才行．

查看解析收藏纠错

+选题
13. 某日小明步行，小颖骑车，他们同时从小颖家出发，以各自的速度匀速到公园去，小颖先到并停留了8分钟，发现相机忘在了家里，于是沿原路以同样的速度回家去取，已知小明的步行速度为180米/分钟，他们各自距离出发点的路程y与出发时间x之间的关系图象如图所示，则当小明到达公园的时候小颖离家米.

查看解析收藏纠错

+选题
14. 白鹤公园风景秀丽，成为广大市民休闲锻炼的圣地星期天，小明和爸爸到白鹤公园登山锻炼，他们同时从山脚出发，以各自的速度匀速登山、前20分钟小明以v₁的速度一直在前，由于小明体力不支，休息了20分钟，这时他发现爸已超过他走在了前面，小明立即以v₂的速度追赶爸爸，直到与爸爸相遇，如图是两人之间相距的路程y（米）与爸爸登山时间x（分）之间的函数图象，则 $\text{[math]}$ ＝.

查看解析收藏纠错

+选题
15. $\text{[math]}$ 三个城市在同一直线上（ $\text{[math]}$ 市在 $\text{[math]}$ 两市之间），甲、乙两车分别从 $\text{[math]}$ 市、 $\text{[math]}$ 市同时出发沿着直线公路相向而行，两车均保持匀速行驶，已知甲车的速度大于乙车的速度，且当甲车到达 $\text{[math]}$ 市时，甲、乙两车都停止运动，甲、乙两车到 $\text{[math]}$ 市的距离之和 $\text{[math]}$ （千米）与甲车行驶的时间 $\text{[math]}$ （小时）之间的关系如图所示，则当乙车到达 $\text{[math]}$ 市时，甲车离 $\text{[math]}$ 市还有千米.

查看解析收藏纠错

+选题
16. 一次函数y=（2a-3）x+a+2（a为常数）的图像，在-1≤x≤1的一段都在x轴上方，则a的取值范围是

查看解析收藏纠错

+选题
17. 表示不超过实数x的最大整数. 在平面上由满足的点所形成的图形的面积是.

查看解析收藏纠错

+选题
18. 在平面直角坐标系中,点P（x₀ ， y₀）到直线Ax+By+C=0的距离公式为: $\text{[math]}$ ,则点P（3，-3）到直线 $\text{[math]}$ 的距离为.

查看解析收藏纠错

+选题
19. 如图是本地区一种产品30天的销售图象，图1是产品日销售量y（单位：件）与时间t（单位：天）的函数关系，图2是一件产品的销售利润z（单位，元）与时间t（单位：天）的函数关系，已知日销售利润=日销售量×一件产品的销售利润，下列正确结论的序号是．

①第24天的销售量为200件；

②第10天销售一件产品的利润是15元；

③第12天与第30天这两天的日销售利润相等；

④第30天的日销售利润是750元．

查看解析收藏纠错

+选题
20. 如图，点A在直线y₁=-x+4上，且位于第一象限．AB⊥x轴于点B，AC⊥y轴于点C，延长CA交直线y₂=- $\text{[math]}$ x+4于点D，连结BC，BD．若 $\text{[math]}$ ，则△BCD 的周长．

查看解析收藏纠错

+选题

21. 如图，在平面直角坐标系xOy中，直线y＝2x＋2与y轴交于点A，与x轴交于点B.直线l⊥x轴负半轴于点C，点D是直线l上一点且位于x轴上方.已知CO＝CD＝4.

（1）求经过A，D两点的直线的函数关系式和点B的坐标；

（2）在直线l上是否存在点P使得△BDP为等腰三角形，若存在，直接写出P点坐标，若不存在，请说明理由.

查看解析收藏纠错

+选题
22.
在平面直角坐标系xOy中，点A（x₁ ， y₁），B（x₂ ， y₂），若x₁x₂+y₁y₂=0，则称A和B互为正交点，即A叫做B的正交点，B也叫做A的正交点。例如：A（1，1），B（2，-2），有1×2+1×（-2）=0，故A和B互为正交点。

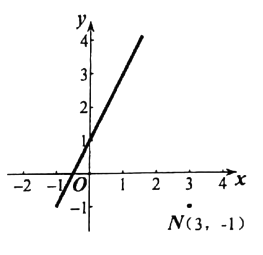
（1）在直角坐标系xOy中，O为坐标原点，判断下列说法是否正确（对的写“正确”，错的写“错误”）。
①原点是任意点的正交点。
②x轴上的任意点与y轴上的任意点都互为正交点。
③点M和N互为正交点，则∠MON=90°.
④点M和N互为正交点，则OM=ON。

（2）点P和Q互为正交点，P的坐标为（2，-3），Q的坐标为（6，m），求m的值。

（3）点M是直线y=2x+1上的一点，点M和N（3，-1）互为正交点，求MN的长度。

查看解析收藏纠错

+选题

23. 有这样一个问题：探究函数 $\text{[math]}$ 的图象与性质．
小东根据学习函数的经验，对函数 $\text{[math]}$ 的图象与性质进行了探究．

下面是小东的探究过程，请补充完成：

（1）化简函数解析式，当 $\text{[math]}$ 时， $\text{[math]}$ ，当 $\text{[math]}$ 时 $\text{[math]}$ ；

（2）根据（1）中的结果，请在所给坐标系中画出函数 $\text{[math]}$ 的图象；备用图

（3）结合画出的函数图象，解决问题：若关于 $\text{[math]}$ 的方程 $\text{[math]}$ 只有一个实数根，直接写出实数a的取值范围：．

查看解析收藏纠错

+选题
24. 甲、乙两城市之间开通了动车组高速列车。已知每隔2h有一列速度相同的动车组列车从甲城开往乙城。如图，OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象。请根据图中的信息，解答下列问题：

（1）从图象看，普通快车发车时间比第一列动车组列车发车时间1h(填“早”或“晚”)，点B的纵坐标600的实际意义是；

（2）请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象；

（3）若普通快车的速度为100km/h，
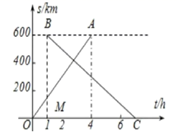
①求BC的表达式，并写出自变量的取值范围；

②第二列动车组列车出发多长时间后与普通快车相遇?

③请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔.

查看解析收藏纠错

+选题
25. 已知直线y=kx+3（1-k）（其中k为常数，k≠0），k取不同数值时，可得不同直线，请探究这些直线的共同特征．

实践操作

（1）当k=1时，直线l₁的解析式为，请在图1中画出图象；当k=2时，直线l₂的解析式为，请在图2中画出图象；

（2）探索发现
直线y=kx+3（1-k）必经过点（，）；

（3）类比迁移
矩形ABCD如图2所示，若直线y=kx+k-2（k≠0）分矩形ABCD的面积为相等的两部分，请在图中直接画出这条直线．

查看解析收藏纠错

+选题

26. 某文具店计划购进A，B两种笔记本共60本，每本A种笔记本比B种笔记本的利润高3元，销售2本A种笔记本与3本B种笔记本所得利润相同，其中A种笔记本的进货量不超过进货总量的 $\text{[math]}$ ，B种笔记本的进货量不超过30本.

（1）每本A种笔记本与B种笔记本的利润各为多少元？

（2）设购进B种笔记本m本，销售总利润为W元，文具店应如何安排进货才能使得W最大？

（3）实际进货时，B种笔记本进价下降n（3≤n≤5）元.若两种笔记本售价不变，请设计出笔记本销售总利润最大的进货方案.

查看解析收藏纠错

+选题
27. 小明从家骑自行车出发，沿着一条直路到相距2400m的邮局办事，小明出发的同时，他的爸爸以96m/min速度从同道路步行回家，在停留2min后沿原路以原速返回，设他们经过tmin时，小明与家之间的距离为s₁m，爸爸与家之间的距离为s₂m，图中折线OABD、线段EF分别表示s₁、s₂与t之间的函数关系的图象.

（1）求s₂与t之间的函数关系式；

（2）小明与爸爸相遇所用的时间？这时他们距离邮局还有多远？

查看解析收藏纠错

+选题
28. 台州市某体育用品商店一次性购进排球、足球两种商品共100个，排球每个进价40元，售价50元，足球每个进价90元，售价105元.

（1）设购进排球x个，销售完此两种商品的总利润为y元，求出y与x的函数关系式；

（2）该商家计划最多投入8000元用于购进此两种商品共100件，至少要购进多少个排球？

（3）在（2）的条件下，若售完这些商品，商家可获得最大利润是多少元？

查看解析收藏纠错

+选题
29.
我县为了倡导居民节约用水，生活用水按阶梯式水价计费，如图是居民每户每月的水费y(元)与所用的水量x（吨）之间的函数图象，请根据图象所提供的信息，解答下列问题：

（1）当用水量不超过10吨时，每吨水收费多少元？

（2）当用水量超过10吨且不超过30吨时，求y与x之间的函数关系式；

（3）某户居民三、四月份水费共82元，四月份用水比三月份多4吨，求这户居民三月份用水多少吨。

查看解析收藏纠错

+选题

湘教版备考2021年中考数学二轮复习专题17一次函数

一、单选题

二、填空题

三、解答题

四、作图题

五、综合题

相关试卷收起∨

湘教版备考2021年中考数学二轮复习专题17一次函数

一、单选题

二、填空题

三、解答题

四、作图题

五、综合题

相关试卷 收起∨

相关试卷收起∨