陕西省咸阳市秦都区2020-2021学年八年级上学期数学期末考试试卷

修改时间：2024-07-13 浏览次数：261 类型：期末考试编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 若 $\text{[math]}$ 不是无理数，则a可以取的值是（）

A . 2 B . 3 C . 4 D . 5

查看解析收藏纠错

+选题
2. 下列选项中，可以用来说明命题“若x²＞9，则x＞3”是假命题的反例是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 下列各组数中，以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为边的三角形不是直角三角形的是（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

查看解析收藏纠错

+选题
4. 已知正比例函数 $\text{[math]}$ ，且 $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小，则该函数的图象经过（）

A . 第二、四象限 B . 第一、三象限 C . 第一、二象限 D . 第二、三象限

查看解析收藏纠错

+选题
5. 如图，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交，已知 $\text{[math]}$ $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 某演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分，然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例计算选手的综合成绩.某选手的演讲内容、演讲能力、演讲效果成绩依次为85、90、95，则该选手的综合成绩为（）

A . 92 B . 88 C . 90 D . 95

查看解析收藏纠错

+选题
7. 若实数 $\text{[math]}$ 、 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ ，则一次函数 $\text{[math]}$ 的图象可能是（）

A . B . C . D .

查看解析收藏纠错

+选题
8. 如图，10块相同的小长方形墙砖拼成一个大长方形，设小长方形墙砖的长为 $\text{[math]}$ 厘米，宽为 $\text{[math]}$ 厘米，则依题意列二元一次方程组正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，在△ABC中，点E和F分别是AC，BC上一点，EF∥AB，∠BCA的平分线交AB于点D，∠MAC是△ABC的外角，若∠MAC＝α，∠EFC＝β，∠ADC＝γ，则α、β、γ三者间的数量关系是（）

A . β＝α+γ B . β＝2γ﹣α C . β＝α+2γ D . β＝2α﹣2γ

查看解析收藏纠错

+选题
10. 某乡村盛产葡萄，果大味美，甲、乙两个葡萄采摘园为吸引游客，在销售价格一样的基础上分别推出优惠方案，甲采摘园的优惠方案：游客进园需购买门票，采摘的所有葡萄按六折优惠．乙采摘园的优惠方案：游客无需买票，采摘葡萄超过一定数量后，超过的部分打折销售．活动期间，某游客的葡萄采摘量为xkg，若在甲采摘园所需总费用为y_甲元，若在乙采摘园所需总费用为y_乙元，y_甲、y_乙与x之间的函数图象如图所示，则下列说法错误的是（）

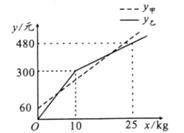
A . 甲采摘园的门票费用是60元 B . 两个采摘园优惠前的葡萄价格是30元/千克 C . 乙采摘园超过10kg后，超过的部分价格是12元/千克 D . 若游客采摘18kg葡萄，那么到甲或乙两个采摘园的总费用相同

查看解析收藏纠错

+选题

二、填空题

11. 小于 $\text{[math]}$ 的最大整数是

查看解析收藏纠错

+选题
12. 如图，在同一直角坐标系中作出一次函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象，则关于 $\text{[math]}$ 、 $\text{[math]}$ 的二元一次方程组 $\text{[math]}$ 的解是.

查看解析收藏纠错

+选题
13. 如图， $\text{[math]}$ ，直线 $\text{[math]}$ 分别交AB、DE于点F、G.若 $\text{[math]}$ ，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
14. 如图，长方体的棱AB长为4，棱BC长为3，棱BF长为2，P为HG的中点，一只蚂蚁从点A出发，沿长方体的表面爬行到点 $\text{[math]}$ 处吃食物，那么它爬行的最短路程是.

查看解析收藏纠错

+选题

三、解答题

15. 计算： $\text{[math]}$ .

查看解析收藏纠错

+选题
16. 解方程组 $\text{[math]}$

查看解析收藏纠错

+选题
17. 已知某正数的两个平方根是 $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ 的立方根为－2，求 $\text{[math]}$ 的算术平方根.

查看解析收藏纠错

+选题
18. 如图，在平面直角坐标系中， $\text{[math]}$ 的三个顶点都在格点上，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .

（1）画出 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的 $\text{[math]}$ ；

（2）在（1）的条件下，分别写出点A、C的对应点 $\text{[math]}$ 、 $\text{[math]}$ 的坐标.

查看解析收藏纠错

+选题
19. 如图，AD是△ABC的中线，AD＝12，AB＝13，BC＝10，求AC长.

查看解析收藏纠错

+选题
20. 如图，在 $\text{[math]}$ 中，∠B=25°，∠BAC=31°，过点A作BC边上的高，交BC的延长线于点D ， CE平分∠ACD ，交AD于点E ．
求：

（1） ∠ACD的度数；

（2） ∠AEC的度数．

查看解析收藏纠错

+选题
21. 如图，直线 $\text{[math]}$ 是一次函数 $\text{[math]}$ 的图象.

（1）求出这个一次函数的解析式；

（2）将该函数的图象向下平移3个单位，求出平移后一次函数的解析式，并写出平移后的图象与 $\text{[math]}$ 轴的交点坐标

查看解析收藏纠错

+选题
22. 如图，已知点E在直线DC上，射线EF平分 $\text{[math]}$ ，过E点作 $\text{[math]}$ ，G为射线EC上一点，连接BG，且 $\text{[math]}$ .

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ ，求证： $\text{[math]}$ .

查看解析收藏纠错

+选题
23. 在一次广场舞比赛中，甲、乙两个队参加表演的女演员的身高（单位：cm）分别是甲队：163 165 165 164 168
乙队：162 164 164 167 168

（1）求甲队女演员身高的平均数、中位数﹑众数；

（2）计算两队女演员身高的方差，并判断哪个队女演员的身高更整齐？

查看解析收藏纠错

+选题

24. 某电器超市销售每台进价为80元、200元的A，B两种型号的电风扇，如表所示是六月份前2周的销售情况：(进价、售价均保持不变，利润=销售收入﹣进货成本)

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	6	5	2100元
第二周	4	10	3400元

（1）求A、B两种型号的电风扇的销售单价.

（2）若超市一共采购这两种型号的电风扇共120台，售完后该超市能否实现利润为8000元的目标？若能，请给出相应的采购方案；若不能，请说明理由.

查看解析收藏纠错

+选题

25. 某工厂新开发生产一种机器，每台机器成本y（万元）与生产数量x（台）之间满足一次函数关系（其中10≤x≤70，且为整数），函数y与自变量x的部分对应值如表

$\text{[math]}$ （单位：台）

10

20

$\text{[math]}$ （单位：万元/台）

60

55

（1）求y与x之间的函数关系式；

（2）市场调查发现，这种机器每月销售量z（台）与售价a（万元/台）之间满足如图所示的函数关系.则当该厂第一个月生产的这种机器40台都按同一售价全部售出，请求出该厂第一个月销售这种机器的总利润.（注：利润＝售价﹣成本）

查看解析收藏纠错

+选题

$\text{[math]}$ （单位：台）	10	20
$\text{[math]}$ （单位：万元/台）	60	55

陕西省咸阳市秦都区2020-2021学年八年级上学期数学期末考试试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨