修改时间:2024-07-13 浏览次数:462 类型:期末考试

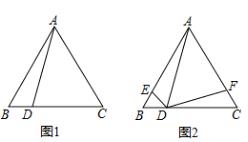
①小明通过观察、实验,提出猜想:在点D运动的过程中,始终有AE = AF,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的两种想法.
想法1:利用AD是∠EDF的平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的相关知识获证.
想法2:利用AD是∠EDF的平分线,构造△ADF的全等三角形,然后通过等腰三角形的相关知识获证
请你参考上面的想法,帮助小明证明AE =AF(一种方法即可).
②小聪在小明的基础上继续进行思考,发现:四边形AEDF的面积与AD的长存在一定的关系.若用S表示四边形AEDF的面积,x表示AD的长,请你直接写出S与x之间的函数表达式.
试题篮