浙江省杭州市滨江区2020年数学中考一模试卷

1. 计算下列各式，结果为负数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 世界上最深的海沟是太平洋的马里亚纳海沟，海拔为 $\text{[math]}$ 米，数据 $\text{[math]}$ 用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图，测得一商店自动扶梯的长为 $\text{[math]}$ ，自动扶梯与地面所成的角为 $\text{[math]}$ ，则该自动扶梯到达的高度 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 某汽车队运送一批救灾物资，若每辆车装4吨，还剩8吨未装；若每辆车装4.5吨，恰好装完.设这个车队有 $\text{[math]}$ 辆车，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 一次中学生田径运动会上，21名参加男子跳高项目的运动员成绩统计如下：

成绩（m)

1.50

1.55

1.60

1.65

1.70

人数

■

8

6

■

1

其中有两个数据被雨水淋湿模糊不清了，则在这组数据中能确定的统计量是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

查看解析收藏纠错

+选题
7. 如图，AB//CD//MN，点M，N分别在线段AD，BC上，AC与MN交于点E，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，AB//CD，点E是直线AB上的点，过点E的直线 $\text{[math]}$ 交直线CD于点F，EG平分 $\text{[math]}$ 交CD于点G，在直线 $\text{[math]}$ 绕点E旋转的过程中，图中 $\text{[math]}$ ， $\text{[math]}$ 的度数可以分别是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，在正方形ABCD中，E是BC边上的点，AE的垂直平分线交CD，AB与点F，G.若 $\text{[math]}$ ，则DF：CF的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 已知二次函数 $\text{[math]}$ （ $\text{[math]}$ 为常数，且 $\text{[math]}$ ）的图像过点 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 的长不小于2，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 因式分解： $\text{[math]}$ .

查看解析收藏纠错

+选题
12. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，CD是 $\text{[math]}$ 的中线，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为.

查看解析收藏纠错

+选题
13. 同时抛掷两枚质地均匀的硬币，两枚硬币全部正面向上的概率是.

查看解析收藏纠错

+选题
14. 如图，圆弧形弯道两边的直道在连接点处与弯道相切，测得 $\text{[math]}$ ，圆弧的半径是2千米，则该段圆弧形歪道的长为千米.（结果保留 $\text{[math]}$ ）

查看解析收藏纠错

+选题
15. 某函数满足自变量 $\text{[math]}$ 时，函数的值 $\text{[math]}$ ，且函数 $\text{[math]}$ 的值始终随自变量 $\text{[math]}$ 的增大而减少，写出一个满足条件的函数表达式.

查看解析收藏纠错

+选题
16. 如图，在等边三角形ABC的AC，BC边上各取一点P，Q，使 $\text{[math]}$ ，AQ，BP相交于点O.若 $\text{[math]}$ ， $\text{[math]}$ ，则AP的长为，AO的长为.

查看解析收藏纠错

+选题

17. 计算

（1） $\text{[math]}$

（2） $\text{[math]}$

查看解析收藏纠错

+选题
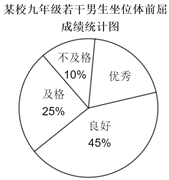
18. 根据《国家学生体质健康标准》规定：九年级男生坐位体前屈达到17.8厘米及以上为优秀；达到13.8厘米至17.7厘米为良好；达到 $\text{[math]}$ 厘米至13.7厘米为及格；达到 $\text{[math]}$ 厘米及以下为不及格.某校为了了解九年级男生的身体柔韧性情况，从该校九年级男生中随机抽取了20%的学生进行坐位体前屈测试，并把测试结果绘制成如图所示的统计表和扇形统计图（部分信息不完整），请根据所给信息解答下列问题.
某校九年级若干男生坐位体前屈的成绩统计表
成绩（厘米）
等级
人数
≥17.8
优秀
a
13.8⁓17.7
良好
b
－0.2⁓13.7
及格
15
≦－0.3
不及格
c

（1）求参加本次坐位体前屈测试人数；

（2）求a、b、c的值；

（3）试估计该年级男生中坐位体前屈成绩不低于13.8厘米的人数.

查看解析收藏纠错

+选题
19. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心，线段 $\text{[math]}$ 的长为半径画弧，与BC边交于点 $\text{[math]}$ ，连接AD，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ .

（1）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

（2）若点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，求证： $\text{[math]}$ .

查看解析收藏纠错

+选题
20. 某游泳池每次换水前后水的体积基本保持不变，当该游泳池以每小时300立方米的速度放水时，经3小时能将池内的水放完，设放水的速度为 $\text{[math]}$ 立方米/时，将池内的水放完需 $\text{[math]}$ 小时.已知该游泳池每小时的最大放水速度为350立方米.

（1）求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式.

（2）若该游泳池将放水速度控制在每小时200立方米至250立方米（含200立方米和250立方米），求放水时间 $\text{[math]}$ 的范围.

（3）该游泳池能否在2.5小时内将池内的水放完？请说明理由.

查看解析收藏纠错

+选题
21. 已知：⊙O的两条弦 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，且 $\text{[math]}$ .

（1）如图1，连接 $\text{[math]}$ ，求证： $\text{[math]}$ .

（2）如图2，在 $\text{[math]}$ ，在 ⌒BD 上取一点 $\text{[math]}$ ，使得 ⌒BE $\text{[math]}$ ⌒BC ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .
①判断 $\text{[math]}$ 与 $\text{[math]}$ 是否相等，并说明理由.

②若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积.

查看解析收藏纠错

+选题
22. 设二次函数 $\text{[math]}$ ，其中 $\text{[math]}$ 为常数，且 $\text{[math]}$ .

（1）当 $\text{[math]}$ 时，试判断点 $\text{[math]}$ 是否在该函数图象上；

（2）若函数的图象经过点 $\text{[math]}$ ，求该函数的表达式；

（3）当 $\text{[math]}$ 时， $\text{[math]}$ 随着 $\text{[math]}$ 的增大而减小，求 $\text{[math]}$ 的取值范围.

查看解析收藏纠错

+选题
23. 如图1，折叠矩形 $\text{[math]}$ ，具体操作：①点 $\text{[math]}$ 为 $\text{[math]}$ 边上一点（不与 $\text{[math]}$ 、 $\text{[math]}$ 重合），把 $\text{[math]}$ 沿 $\text{[math]}$ 所在的直线折叠， $\text{[math]}$ 点的对称点为 $\text{[math]}$ 点；②过点 $\text{[math]}$ 对折 $\text{[math]}$ ，折痕 $\text{[math]}$ 所在的直线交 $\text{[math]}$ 于点 $\text{[math]}$ 、 $\text{[math]}$ 点的对称点为 $\text{[math]}$ 点.

（1）求证： $\text{[math]}$ ∽ $\text{[math]}$ .

（2）若 $\text{[math]}$ ， $\text{[math]}$ .
①点 $\text{[math]}$ 在移动的过程中，求 $\text{[math]}$ 的最大值.

②如图2，若点 $\text{[math]}$ 恰在直线 $\text{[math]}$ 上，连接 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题

浙江省杭州市滨江区2020年数学中考一模试卷

一、选择题（每小题3分，共30分）

二、填空题（本大题共6个小题，每小题4分，共24分）

三、解答题（本大题共7个小题，共66分）

相关试卷收起∨

某校九年级若干男生坐位体前屈的成绩统计表
成绩（厘米）	等级	人数
≥17.8	优秀	a
13.8⁓17.7	良好	b
－0.2⁓13.7	及格	15
≦－0.3	不及格	c

成绩（m)	1.50	1.55	1.60	1.65	1.70
人数	■	8	6	■	1

浙江省杭州市滨江区2020年数学中考一模试卷

一、选择题（每小题3分，共30分）

二、填空题（本大题共6个小题，每小题4分，共24分）

三、解答题（本大题共7个小题，共66分）

相关试卷 收起∨

相关试卷收起∨