湖北省黄石市阳新县陶港中学2020年九年级数学中考二模试卷

修改时间：2024-07-13 浏览次数：248 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 一个数的倒数是-2，则这个数是（）

A . -2 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列计算正确的是（）

A . a²·a³＝a⁵ B . （a²）³＝a⁵ C . a¹⁰÷a²＝a⁵ D . 2a⁵－a⁵＝2

查看解析收藏纠错

+选题
3. 1天24小时共有86400秒，用科学记数法可表示为（保留两个有效数字）（）

A . $\text{[math]}$ 秒 B . $\text{[math]}$ 秒 C . $\text{[math]}$ 秒 D . $\text{[math]}$ 秒

查看解析收藏纠错

+选题
4. 从甲，乙，丙三人中任选一名代表，甲被选中的可能性是（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 在 $\text{[math]}$ 方格纸中将图（1）中的图形 $\text{[math]}$ 平移后的位置如图（2）中所示，那么正确的平移方法是（）
（1）（2）

A . 先向下移动 $\text{[math]}$ 格，再向左移动 $\text{[math]}$ 格； B . 先向下移动 $\text{[math]}$ 格，再向左移动 $\text{[math]}$ 格； C . 先向下移动 $\text{[math]}$ 格，再向左移动 $\text{[math]}$ 格； D . 先向下移动 $\text{[math]}$ 格，再向左移动 $\text{[math]}$ 格。

查看解析收藏纠错

+选题
6. 某青年排球队12名队员的年龄情况如下：

年龄（单位：岁）

18

19

20

21

22

人数

1

4

3

2

2

则12名队员的年龄（）

A . 众数是20岁，中位数是19岁 B . 众数是19岁，中位数是19岁 C . 众数是19岁，中位数是20.5岁 D . 众数是19岁，中位数是20岁

查看解析收藏纠错

+选题
7.
如图，一个圆柱形笔筒，量得笔筒的高是20cm，底面圆的半径为5cm，那么笔筒的侧面积为（　　）

A . 200cm² B . 100πcm² C . 200πcm² D . 500πcm²

查看解析收藏纠错

+选题
8. 如图所示：边长分别为 $\text{[math]}$ 和 $\text{[math]}$ 的两个正方形，其一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为 $\text{[math]}$ ，大正方形内除去小正方形部分的面积为 $\text{[math]}$ （阴影部分），那么 $\text{[math]}$ 与 $\text{[math]}$ 的大致图象应为（）．

A . B . C . D .

查看解析收藏纠错

+选题

二、填空题

9. 分解因式： $\text{[math]}$ =.

查看解析收藏纠错

+选题
10. 若关于x的方程 $\text{[math]}$ 有实数根，则K的取值范围是.

查看解析收藏纠错

+选题
11. 小明同学测量一个光盘的直径，他只有一把直尺和一块三角尺，他将直尺、光盘和三角尺按图所示方法放置于桌面上，并量出AB＝3 cm ，则此光盘的直径是 cm.

查看解析收藏纠错

+选题
12. 定义：平面中两条直线 $\text{[math]}$ 和 $\text{[math]}$ 相交于点O，对于平面上任意一点M,若p,q分别是M到直线 $\text{[math]}$ 和 $\text{[math]}$ 的距离，则称有序非负实数对 $\text{[math]}$ 是点M的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是.

查看解析收藏纠错

+选题

三、解答题

13. 计算： $\text{[math]}$

查看解析收藏纠错

+选题
14. 解方程组： $\text{[math]}$

查看解析收藏纠错

+选题
15. 化简： $\text{[math]}$

查看解析收藏纠错

+选题
16. 如图，将矩形纸片ABCD沿对角线AC折叠，使点B落在点E处，求证：EF=DF.

查看解析收藏纠错

+选题
17.
三根垂直地面的木杆甲、乙、丙，在路灯下乙、丙的影子如图所示．试确定路灯灯泡的位置，再作出甲的影子．（不写作法，保留作图痕迹）

查看解析收藏纠错

+选题
18. 如图，在ΔABC中，∠C=90°，点D在BC上，BD=4，AD=BC，cos∠ADC= $\text{[math]}$ .

（1）求DC的长；

（2）求sinB的值.

查看解析收藏纠错

+选题
19. 如图是不倒翁的正视图，不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B，不倒翁的鼻尖正好是圆心O.

（1）若∠OAB=25°，求∠APB的度数；

（2）若∠OAB=n°，请直接写出∠APB的度数.

查看解析收藏纠错

+选题

20. 为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图，解答下列问题：

（1）填充频率分布表中的空格；

（2）补全频率分布直方图；

（3）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？（不要求说明理由）

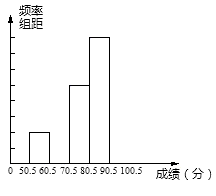
频率分布表
分组	频数	频率
50.5～60.5	4	0.08
60.5～70.5	8	0.16
70.5～80.5	10	0.20
80.5～90.5	16	0.32
90.5～100.5
合计

查看解析收藏纠错

+选题

21. 个人发表文章、出版图书所得稿费的纳税计算方法是：（1）稿费不高于800元的不纳税；（2）稿费高于800元而不高于4000元，缴纳超过800元部分稿费的14％；（3）稿费超过4000元的，缴纳全部稿费的11％.张老师得到一笔稿费，缴纳个人所得税420元，问张老师的这笔稿费是多少元？

查看解析收藏纠错

+选题
22. 现有一张长和宽之比为2：1的长方形纸片.将它折两次（第一次折后也可以打开铺平再折第二次）.使得折痕将纸片分为面积相等且不重叠的四个部分（称为一个操作），如图甲（虚线表示折痕）.

除图甲外，请你再给出三个不同的操作，分别将折痕画在图①至图③中（规定：一个操作得到的四个图形，和另一个操作得到的四个图形，如果能够“配对”得到四组全等的图形，那么就认为是相同的操作.如图乙和图甲是相同的操作）.

图① 图② 图③

查看解析收藏纠错

+选题
23. 如图，Rt△ABC中，∠C=90°，∠B的平分线交AC于E，DE⊥BE.

（1）试说明AC是△BED外接圆的切线；

（2）若CE=1，BC=2，求△ABC内切圆的面积.

查看解析收藏纠错

+选题
24. 研究发现，二次函数 $\text{[math]}$ （ $\text{[math]}$ ）图象上任何一点到定点（0， $\text{[math]}$ ）和到定直线 $\text{[math]}$ 的距离相等.我们把定点（0， $\text{[math]}$ ）叫做抛物线 $\text{[math]}$ 的焦点，定直线 $\text{[math]}$ 叫做抛物线 $\text{[math]}$ 的准线.

（1）写出函数 $\text{[math]}$ 图象的焦点坐标和准线方程；

（2）等边三角形OAB的三个顶点都在二次函数 $\text{[math]}$ 图象上，O为坐标原点，求等边三角形的边长；

（3） M为抛物线 $\text{[math]}$ 上的一个动点，F为抛物线 $\text{[math]}$ 的焦点，P（1，3）为定点，求MP+MF的最小值.

查看解析收藏纠错

+选题
25. 我们做如下的规定：如果一个三角形在运动变化时保持形状和大小不变，则把这样的三角形称为三角形板.
把两块边长为4的等边三角形板 $\text{[math]}$ 和 $\text{[math]}$ 叠放在一起，使三角形板 $\text{[math]}$ 的顶点 $\text{[math]}$ 与三角形板 $\text{[math]}$ 的AC边中点 $\text{[math]}$ 重合，把三角形板 $\text{[math]}$ 固定不动，让三角形板 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转，设射线 $\text{[math]}$ 与射线 $\text{[math]}$ 相交于点M，射线 $\text{[math]}$ 与线段 $\text{[math]}$ 相交于点N.

（1）如图1，当射线 $\text{[math]}$ 经过点 $\text{[math]}$ ，即点N与点 $\text{[math]}$ 重合时，易证△ADM∽△CND.此时，AM·CN=.

（2）将三角形板 $\text{[math]}$ 由图1所示的位置绕点 $\text{[math]}$ 沿逆时针方向旋转，设旋转角为 $\text{[math]}$ .其中 $\text{[math]}$ ，问AM·CN的值是否改变？说明你的理由.

（3）在（2）的条件下，设AM= x，两块三角形板重叠面积为 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式.（图2，图3供解题用）

查看解析收藏纠错

+选题

年龄（单位：岁）	18	19	20	21	22
人数	1	4	3	2	2

湖北省黄石市阳新县陶港中学2020年九年级数学中考二模试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨