修改时间:2024-07-13 浏览次数:235 类型:中考模拟
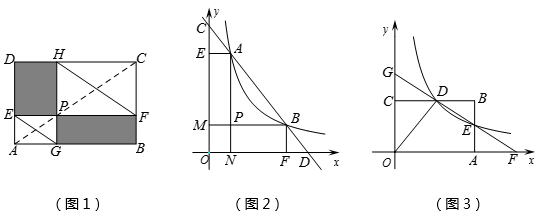
如图1,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H,容易证明四边形PEDH和四边形PFBG是面积相等的矩形,分别连结EG,FH.
①根据矩形PEDH和矩形PFBG面积相等的关系,那么PE·PH= ▲ .
②求证:EG∥FH.
如图2,已知直线 分别与x轴,y轴交于D,C两点,
与双曲线 交于A,B两点. 求证:AC=BD.
如图3,反比例函数 (x>0)的图象与矩形ABCO的边BC交于点D,与边AB交于点E, 直线DE与x轴,y轴分别交于点F,G . 若矩形ABCO的面积为10,△ODG与△ODF的面积比为3:5,则k=.
试题篮