四川省简阳市简城学区、镇金学区2018-2019学年七年级下学期数学期中考试试卷

修改时间：2024-07-13 浏览次数：316 类型：期中考试编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 目前，世界上能制造出的最小晶体管的长度只有0.000 000 04m，将0.000 000 04用科学记数法表示为（）

A . 4×10⁸ B . 4×10^﹣⁸ C . 0.4×10⁸ D . ﹣4×10⁸

查看解析收藏纠错

+选题
2. 下面是一名学生所做的4道练习题：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ 。他做对的个数是（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
3. 下列各式中，计算结果正确是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 小明在利用完全平方公式计算一个二项整式的平方时，不小心用墨水把最后一项染黑了，得到正确结果变为 $\text{[math]}$ （），你觉得这一项应是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图，通过计算大正方形的面积，可以验证的公式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6.
如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（　　）

A . 30° B . 25° C . 20° D . 15°

查看解析收藏纠错

+选题
7. 如图，已知∠1=∠B，∠2=∠C，则下列结论不成立的是（）

A . AB//CD B . AD//BC C . ∠2+∠B=180° D . ∠B=∠C

查看解析收藏纠错

+选题
8. 下列正确说法的个数是（）
①同位角相等；②等角的补角相等；③两直线平行，同旁内角相等；④在同一平面内，过一点有且只有一条直线与已知直线垂直.

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
9. 弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂重物的质量x（kg）有下面的关系，那么弹簧总长y（cm）与所挂重物x（kg）之间的关系式为（）

x（kg）

0

1

2

3

4

5

6

y（cm）

12

12.5

13

13.5

14

14.5

15

A . y=0.5x+12 B . y=x+10.5 C . y=0.5x+10 D . y=x+12

查看解析收藏纠错

+选题
10. 如图，在△ABC中，AC＝BC，有一动点P从点A出发，沿A→C→B→A匀速运动，则CP的长度s与时间t之间的函数关系用图象描述大致是（）

A . B . C . D .

查看解析收藏纠错

+选题

二、填空题

11. 若长方形的面积是3a²+2ab+3a，长为3a，则它的宽为．

查看解析收藏纠错

+选题
12. 已知 $\text{[math]}$ ，则 n= .

查看解析收藏纠错

+选题
13. 若∠1与∠2互补，∠3与30°互余，∠2+∠3=200°，则∠1=度.

查看解析收藏纠错

+选题
14. 已知m﹣n=2，mn=﹣1，则（1+2m）（1﹣2n）的值为．

查看解析收藏纠错

+选题
15. 若多项式5x²+2x﹣2与多项式ax+1的乘积中，不含x²项，则常数a=．

查看解析收藏纠错

+选题
16. 2（1+ $\text{[math]}$ ）（1+ $\text{[math]}$ ）（1+ $\text{[math]}$ ）（1+ $\text{[math]}$ ）+ $\text{[math]}$ =．

查看解析收藏纠错

+选题
17. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D，C分别在M，N的位置上，若∠EFG=56°，则∠1=，∠2=．

查看解析收藏纠错

+选题
18. 已知（a-4）（a-2）=3，则（a-4）²+（a-2）²的值为．

查看解析收藏纠错

+选题
19. 若规定符号 $\text{[math]}$ $\text{[math]}$ 的意义是： $\text{[math]}$ $\text{[math]}$ = ，则当m²﹣2m﹣3=0时， $\text{[math]}$ $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题

三、解答题

20. 计算题

（1）计算： $\text{[math]}$

（2）计算： $\text{[math]}$

（3）用乘法公式计算： $\text{[math]}$

查看解析收藏纠错

+选题
21. 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ，n=2.

查看解析收藏纠错

+选题
22. 已知 $\text{[math]}$ ， $\text{[math]}$ ，求下列式子的值：

（1） $\text{[math]}$ ；

（2） 6ab.

查看解析收藏纠错

+选题
23.
如图，直线AB∥CD，BC平分∠ABD，∠1=65°，求∠2的度数．

查看解析收藏纠错

+选题
24. 如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F.

（1） CD与EF平行吗？为什么？

（2）如果∠1＝∠2，试判断DG与BC的位置关系，并说明理由.

查看解析收藏纠错

+选题
25. 周末，小明坐公交车到滨海公园游玩，他从家出发0.8小时后达到中心书城，逗留一段时间后继续坐公交车到滨海公园，小明离家一段时间后，爸爸驾车沿相同的路线前往海滨公园.如图是他们离家路程s（km）与小明离家时间t（h）的关系图，请根据图回答下列问题：

（1）图中自变量是，因变量是；

（2）小明家到滨海公园的路程为km，小明在中心书城逗留的时间为h；

（3）小明出发小时后爸爸驾车出发；

（4）图中A点表示；

（5）小明从中心书城到滨海公园的平均速度为km/h，小明爸爸驾车的平均速度为km/h；（补充；爸爸驾车经过追上小明）；

（6）小明从家到中心书城时，他离家路程s与坐车时间t之间的关系式为.

查看解析收藏纠错

+选题
26. “化归与转化的思想”是指在研究解决数学问题时采用某种手段将问题通过变换使之转化，进而使问题得到解决。

（1）我们知道 $\text{[math]}$ 可以得到 $\text{[math]}$ 。如果 $\text{[math]}$ ，求 $\text{[math]}$ 、 $\text{[math]}$ 的值.

（2）已知 $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ 试问多项式a²+b²+c²﹣ab﹣ac﹣bc的值是否与变量 $\text{[math]}$ 的取值有关？若有关请说明理由；若无关请求出多项式的值.

（3）你认为图2中的阴影部分的正方形的边长等于.

（4）请用两种不同的方法求图2中阴影部分的面积.

（5）仔细观察图2，写出 $\text{[math]}$ 三个代数式之间的等量关系.

（6）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
27. 如图1，是一个长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形。

（1）我们知道 $\text{[math]}$ 可以得到 $\text{[math]}$ 。如果 $\text{[math]}$ ，求 $\text{[math]}$ 、 $\text{[math]}$ 的值.

（2）已知 $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ 试问多项式a²+b²+c²﹣ab﹣ac﹣bc的值是否与变量 $\text{[math]}$ 的取值有关？若有关请说明理由；若无关请求出多项式的值.

（3）你认为图2中的阴影部分的正方形的边长等于.

（4）请用两种不同的方法求图2中阴影部分的面积.

（5）仔细观察图2，写出 $\text{[math]}$ 三个代数式之间的等量关系.

（6）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
28. 如图，直线l₁∥l₂ ，直线l与l₁、l₂分别交于A、B两点，点M、N分别在l₁、l₂上，点M、N、P均在l的同侧（点P不在l₁、l₂上），若∠PAM=α，∠PBN=β．

（1）当点P在l₁与l₂之间时．
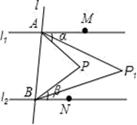
①求∠APB的大小（用含α、β的代数式表示）；

②若∠PAM的平分线与∠PBN的平分线交于点P₁ ， ∠P₁AM的平分线与∠P₁BN的平分线交于点P₂ ， …，∠P_n_﹣₁AM的平分线与∠P_n_﹣₁BN的平分线交于点P_n ，则∠AP₁B=，∠AP_nB=．（用含α、β的代数式表示，其中n为正整数）

（2）当点P不在l₁与l₂之间时．
若∠PAM的平分线与∠PBN的平分线交于点P₁ ， ∠P₁AM的平分线与∠P₁BN的平分线交于点P₂ ， …，∠P_n_﹣₁AM的平分线与∠P_n_﹣₁BN的平分线交于点P_n ，请直接写出∠AP_nB的大小．（用含α、β的代数式表示，其中n为正整数）

查看解析收藏纠错

+选题

x（kg）	0	1	2	3	4	5	6
y（cm）	12	12.5	13	13.5	14	14.5	15

四川省简阳市简城学区、镇金学区2018-2019学年七年级下学期数学期中考试试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨