2017年河南省普通高中中考数学模拟试卷（导向一）

1. ﹣5的倒数是（）

A . $\text{[math]}$ B . 5 C . ﹣ $\text{[math]}$ D . ﹣5

查看解析收藏纠错

+选题
2. 2016年8月25日，有媒体报道说，国家发展和改革委员会近日对外发布了推进东北振兴三年滚动实施方案，其中涉及到国家将在东北投入1.6万亿元人民币资金，则1.6万用科学记数法表示为（）

A . 1.6×10¹² B . 1.6×10¹⁰ C . 1.6×10⁴ D . 1.6×10³

查看解析收藏纠错

+选题
3. 某校调查了20名同学某一周玩手机游戏的次数，调查结果如下表所示，那么这20名同学玩手机游戏次数的平均数为（）
次数
2
4
5
8
人数
2
2
10
6

A . 5 B . 5.5 C . 6 D . 6.5

查看解析收藏纠错

+选题
4. 如果2m⁹^﹣^xn^y和﹣3m^2yn^3x⁺¹是同类项，则2m⁹^﹣^xn^y+（﹣3m^2yn^3x⁺¹）=（）

A . ﹣m⁸n⁴ B . mn⁴ C . ﹣m⁹n D . 5m³n²

查看解析收藏纠错

+选题
5. 若关于x的分式方程 $\text{[math]}$ + $\text{[math]}$ =1有增根，则m的值是（）

A . m=0或m=3 B . m=3 C . m=0 D . m=﹣1

查看解析收藏纠错

+选题
6. 把n边形变为（n+x）边形，内角和增加了720°，则x的值为（）

A . 4 B . 6 C . 5 D . 3

查看解析收藏纠错

+选题
7. 现有四张完全相同的卡片，上面分别标有数字1，4，5，7，把卡片背面朝上洗匀，两个人依次从中随机抽取一张卡片不放回，则这两个人抽取的卡片上的数字都是奇数的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 已知x＞y，若对任意实数a，以下结论：
甲：ax＞ay；乙：a²﹣x＞a²﹣y；丙：a²+x≤a²+y；丁：a²x≥a²y
其中正确的是（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题
9. 如图，四边形纸片ABCD中，∠A=70°，∠B=80°，将纸片折叠，使C，D落在AB边上的C′，D′处，折痕为MN，则∠AMD′+∠BNC′=（）

A . 50° B . 60° C . 70° D . 80°

查看解析收藏纠错

+选题
10.
如图，等边△ABC边长为2，四边形DEFG是平行四边形，DG=2，DE=3，∠GDE=60°，BC和DE在同一条直线上，且点C与点D重合，现将△ABC沿D→E的方向以每秒1个单位的速度匀速运动，当点B与点E重合时停止，则在这个运动过程中，△ABC与四边形DEFG的重合部分的面积S与运动时间t之间的函数关系图象大致是（）

A . B . C . D .

查看解析收藏纠错

+选题

11. 计算：|﹣ $\text{[math]}$ |+3^﹣²=．

查看解析收藏纠错

+选题
12. 已知x=﹣2是关于x的方程x²﹣2ax+a²=0的一个根，则a的值为．

查看解析收藏纠错

+选题
13. △ABC三个顶点的坐标分别为A（2，2），B（4，2），C（6，6），在此直角坐标系中作△DEF，使得△DEF与△ABC位似，且以原点O为位似中心，位似比为1：2，则△DEF的面积为．

查看解析收藏纠错

+选题
14. 如图，过⊙O外一点P向⊙O作两条切线，切点分别为A，B，若⊙O半径为2，∠APB=60°，则图中阴影部分的面积为．

查看解析收藏纠错

+选题
15. 如图，矩形ABCD中，AD=5，AB=6，点E为DC上一个动点，把△ADE沿AE折叠，点F为CD上一个动点，把△BCF沿BF折叠，当点D的对应点和点C的对应点都落在点D′处时，EF的长为．

查看解析收藏纠错

+选题

16. 根据所示的程序，若输入x的值是方程x²﹣2x﹣3=0的解，求输出D的值．

查看解析收藏纠错

+选题
17. 如图，在平面直角坐标系中，点A坐标为（0，3），点B在x轴上

（1）在坐标系中求作一点M，使得点M到点A，点B和原点O这三点的距离相等，在图中保留作图痕迹，不写作法；

（2）若函数y= $\text{[math]}$ 的图象经过点M，且sin∠OAB= $\text{[math]}$ ，求k的值．

查看解析收藏纠错

+选题
18. 如图，AB是⊙O的直径，点P是AB下方的半圆上不与点A，B重合的一个动点，点C为AP中点，延长CO交⊙O于点D，连接AD，过点D作⊙O的切线交PB的廷长线于点E，连CE交AB于点F，连接DF．

（1）求证：△DAC≌△ECP；

（2）填空：
①四边形ACED是何种特殊的四边形？
②在点P运动过程中，线段DF、AP的数量关系是 $\text{[math]}$ ．

查看解析收藏纠错

+选题
19.
在一节数学活动课上，王老师将本班学生身高数据（精确到1厘米）出示给大家，要求同学们各自独立绘制一幅频数分布直方图，甲绘制的如图①所示，乙绘制的如图②所示，经王老师批改，甲绘制的图是正确的，乙在数据整理与绘图过程中均有个别错误．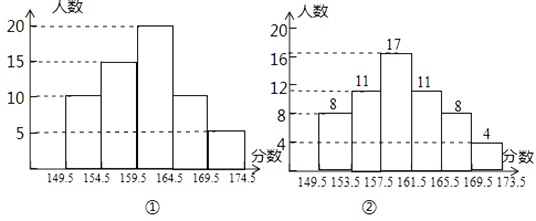

（1）写出乙同学在数据整理或绘图过程中的错误（写出一个即可）；

（2）甲同学在数据整理后若用扇形统计图表示，则159.5﹣164.5这一部分所对应的扇形圆心角的度数为；

（3）该班学生的身高数据的中位数是；

（4）假设身高在169.5﹣174.5范围的5名同学中，有2名女同学，班主任老师想在这5名同学中选出2名同学作为本班的正、副旗手，那么恰好选中一名男同学和一名女同学当正，副旗手的概率是多少？

查看解析收藏纠错

+选题
20.
如图，明亮同学在点A处测得大树顶端C的仰角为36°，斜坡AB的坡角为30°，沿在同一剖面的斜坡AB行走16米至坡顶B处，然后再沿水平方向行走6.4米至大树脚底点D处，那么大树CD的高度约为多少米？）（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73， $\text{[math]}$ ≈1.7）．

查看解析收藏纠错

+选题
21. 一家商店进行装修，若请甲、乙两个装修组同时施工，8天可以完成，需付两组费用共3520元，若先请甲组单独做6天，再请乙组单独做12天可以完成，需付费用3480元，问：

（1）甲、乙两组工作一天，商店各应付多少钱？

（2）已知甲单独完成需12天，乙单独完成需24天，单独请哪个组，商店所需费用最少？

（3）若装修完后，商店每天可赢利200元，你认为如何安排施工更有利于商店？请你帮助商店决策．（可用（1）（2）问的条件及结论）

查看解析收藏纠错

+选题
22. 定义：点M，N把线段AB分割成AM、MN，NB，若以AM、MN、NB为边的三角形是一个直角三角形，则称点M、N是线段AB的勾股分割点．

（1）
如图①，已知M、N是线段AB的勾股分割点，AM=6，MN=8，求NB的长；

（2）
如图②，在△ABC中，点D、E在边线段BC上，且BD=3，DE=5，EC=4，直线l∥BC，分别交AB、AD、AE、AC于点F、M、N、G．求证：点M，N是线段FG的勾股分割点

（3）
在菱形ABCD中，∠ABC=β（β＜90°），点E、F分别在BC、CD上，AE、AF分别交BD于点M、N．
①如图③，若BE= $\text{[math]}$ BC，DF= $\text{[math]}$ CD，求证：M、N是线段BD的勾股分割点．
②如图④，若∠EAF= $\text{[math]}$ ∠BAD，sinβ= $\text{[math]}$ ，当点M、N是线段AB的勾股分割点时，求BM：MN：ND的值．

查看解析收藏纠错

+选题
23.
如图，直线y=﹣ $\text{[math]}$ x+4交x轴于点A，交y轴于点C，抛物线y=ax²﹣ $\text{[math]}$ x+c过点A，交y轴于点B（0，﹣2）

（1）求抛物线的解析式；

（2）点M为抛物线在第四象限部分上的一个动点，求四边形BMAC面积的最大值；

（3）点D为抛物线对称轴上一点，规定：d=|AD﹣BD|，探究d是否存在最大值？若存在，请直接写出d的最大值及此时点D的坐标．

查看解析收藏纠错

+选题

2017年河南省普通高中中考数学模拟试卷（导向一）

一、选择题

二、填空题

三、解答题

相关试卷收起∨

次数	2	4	5	8
人数	2	2	10	6

2017年河南省普通高中中考数学模拟试卷（导向一）

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨