修改时间:2024-07-13 浏览次数:337 类型:期中考试

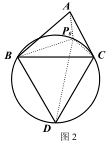

①如图 1,已知点 P 为等边△ABC 外接圆的弧BC 上任意一点.求证:PB+PC= PA.
②定义:在△ABC 所在平面上存在一点 P,使它到三角形三顶点的距离之和最小,则称点 P 为△ABC的费马点,此时 PA+PB+PC 的值为△ABC 的费马距离.
①我们有如下探寻△ABC (其中∠A,∠B,∠C 均小于 120°)的费马点和费马距离的方法:
如图 2,在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆,根据(1)的结论,易知线段▲ 的长度即为△ABC 的费马距离.
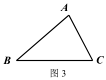
②在图 3 中,用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
①判断题(正确的打√,错误的打×):
ⅰ.任意三角形的费马点有且只有一个( );
ⅱ.任意三角形的费马点一定在三角形的内部( ).
②已知正方形 ABCD,P 是正方形内部一点,且 PA+PB+PC 的最小值为 ,求正方形 ABCD 的
边长.
试题篮