修改时间:2024-07-13 浏览次数:691 类型:中考真卷
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:把边长为4的正方形纸片ABCD对折,使边AB与CD重合,展开后得到折痕EF,如图①;点M为CF上一点,将正方形纸片ABCD沿直线DM折叠,使点C落在EF上的点N处,展开后连接DN,MN,AN,如图②.
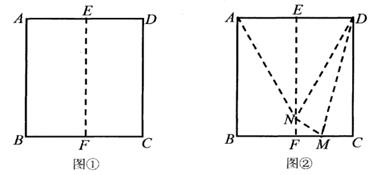
图②中,∠CMD= °;线段NF= ;
剪一剪、折一折:将图②中的△AND剪下来,将其沿直线GH折叠,使点A落在点A’处,分别得到图③、图④.
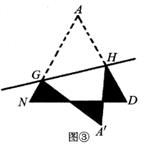
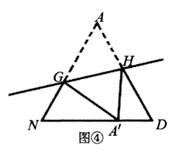
图③中阴影部分的周长为;
试题篮