修改时间:2024-07-31 浏览次数:321 类型:月考试卷
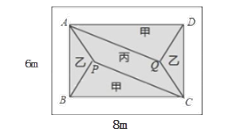
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.

|
ɑ |
30° |
40° |
50° |
60° |
|
β |
120° |
130° |
140° |
150° |
|
γ |
150° |
140° |
130° |
120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并结合图形分别给出证明.
试题篮