题型:填空题 题类:常考题 难易度:普通
贵州省黔西南州兴义市2017-2018学年七年级下学期数学期中考试试卷
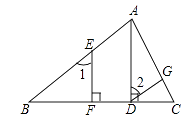
已知AD BC,EF
BC,
1=
2.
求证:DG//BA.
证明:因为AD BC.EF
BC(已知).
所以 EFB=
ADB=
,
所以 EFB=
ADB(等量代换),
所以EF//AD,
所以 1=
BAD,
又因为 1=
2(已知),
所以 =
(等量代换),
所以DG//BA.
试题篮