题型:综合题 题类:常考题 难易度:困难
吉林省辽源市2018-2019学年九年级上学期数学期末考试试卷
下面是小颖对一道题目的解答.
题目:如图,
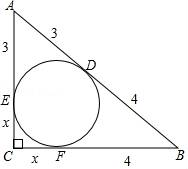
Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.
解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.
根据切线长定理,得AE=AD=3,BF=BD=4,CF=CE=x.
根据勾股定理,得(x+3)2+(x+4)2=(3+4)2 .
整理,得x2+7x=12.
所以S△ABC= AC
BC
= (x+3)(x+4)
= (x2+7x+12)
= ×(12+12)
=12.
小颖发现12恰好就是3×4,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知:△ABC的内切圆与AB相切于点D,AD=m,BD=n.
可以一般化吗?
试题篮