题型:综合题 题类:常考题 难易度:困难
江苏省响水县2018-2019学年八年级上学期数学期末考试试卷
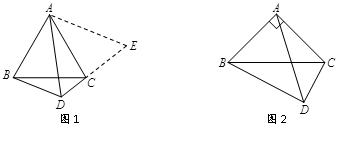
解题思路:延长DC到点E,使CE=BD,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是;(直接写出结果)

【问题提出】小明在做作业本时发现利用右图可以证明勾股定理.思路为利用面积法,将梯形的面积用不同的方式表示列出等式.由此猜想如果将Rt△DAF向左平移,能否证明勾股定理?
【方案设计】考虑到探究的难度,他首先设计了两种特殊的位置,开展研究:
方案 | 方案一 | 方案二 |
图形 |
|
|
备注 | Rt△BCA≌Rt△EAD | Rt△BCA≌Rt△CFD |
BC=a , AC=b , AB=c | ||
【探究验证】首先验证方案一为方案二提供经验基础.
方式 | 验证过程 (分别用含有a , b , c的代数式完成填空) | 图形 |
方式① | S四边形ADBE=S△ABE +S△ABD S△ABE = ▲ . (以AE为底,高为BC) S△ABD = ▲ . (以AD为底,则AD边上的高与AC等长) | 连结BE , BD,不难得出AB⊥ED
|
方式② | S四边形ADBE =S△EBD +S△EAD
|
综上所述利用方式①,②列出等式即可证明勾股定理.
【方法应用】
根据上述经验,请你继续完成方案二后续的证明过程.
提示:如图,连结BD , AD , 不难得出CD⊥BA , 利用两种方法表示四边形BCAD的面积.

试题篮