湘教版数学九年级上册《第3章图形的相似》单元测试B卷

修改时间：2021-09-15 浏览次数：225 类型：单元试卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . 2 B . 4 C . 6 D . 8

查看解析收藏纠错

+选题
2. 下列四组线段中，是成比例线段的是（）

A . 2cm，3cm，4cm，5cm B . 3cm，6cm，0.2dm，5cm C . 2cm，4cm，6cm，8cm D . 12cm，8cm，15cm，10cm

查看解析收藏纠错

+选题
3. 如图，在正方形ABCD中，E，F是对角线AC上的两点，且EF＝2AE＝2CF，连接DE并延长交AB于点M，连接DF并延长交BC于点N，连接MN，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图，矩形OABC的面积为36，它的对角线OB与双曲线y $\text{[math]}$ 相交于点D ，且OD：OB＝2：3，则k的值为（）

A . 12 B . ﹣12 C . 16 D . ﹣16

查看解析收藏纠错

+选题
5. 如图，四边形ABCD是平行四边形，点E在CD边上，则下列结论错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图， $\text{[math]}$ 、 $\text{[math]}$ 交于 $\text{[math]}$ 点， $\text{[math]}$ ，则下列结论一定正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，在平面直角坐标系中，矩形 $\text{[math]}$ 与矩形 $\text{[math]}$ 是以点 $\text{[math]}$ 为位似中心的位似图形，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A . 3 B . 4 C . 4.5 D . 6

查看解析收藏纠错

+选题
8. 如图，将 $\text{[math]}$ 沿 $\text{[math]}$ 边向右平移得到 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点G.若 $\text{[math]}$ . $\text{[math]}$ .则 $\text{[math]}$ 的值为（）

A . 2 B . 4 C . 6 D . 8

查看解析收藏纠错

+选题
9. 下列四个命题：①直径是圆的对称轴；②若两个相似四边形的相似比是1：3，则它们的周长比是1：3，面积比是1：6；③同一平面内垂直于同一直线的两条直线互相平行；④对角线相等且互相垂直的平行四边形是正方形.其中真命题有（）

A . ①③ B . ①④ C . ③④ D . ②③④

查看解析收藏纠错

+选题
10. 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，使 $\text{[math]}$ ，连结CE，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

查看解析收藏纠错

+选题
11. 如图，在平面直角坐标系中，将 $\text{[math]}$ 以原点O为位似中心放大后得到 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的相似比是（）

A . 2：1 B . 1：2 C . 3：1 D . 1：3

查看解析收藏纠错

+选题
12. 如图，平行四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点E，点O为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 并延长，交 $\text{[math]}$ 的延长线于点D，交 $\text{[math]}$ 于点G，连接 $\text{[math]}$ 、 $\text{[math]}$ ，若平行四边形 $\text{[math]}$ 的面积为48，则 $\text{[math]}$ 的面积为（）

A . 5.5 B . 5 C . 4 D . 3

查看解析收藏纠错

+选题

二、填空题

13. 若 $\text{[math]}$ ，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
14. 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是成比例线段，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则线段 $\text{[math]}$ $\text{[math]}$ .

查看解析收藏纠错

+选题
15. 如图，△ABC中，AB＝AC，∠B＝72°，∠ACB的平分线CD交AB于点D，则点D是线段AB的黄金分割点.若AC＝2，则BD＝.

查看解析收藏纠错

+选题
16. 如图，矩形ABCD中，AD $\text{[math]}$ AB ，点E在BC边上，且AE=AD ， DF⊥AE于点F ，连接DE ， BF ， BF的延长线交DE于点O ，交CD于点G ．以下结论：①AF=DC ， ②OF：BF=CE：CG ， ③S_△BCG $\text{[math]}$ S_△DFG ， ④图形中相似三角形有6对，则正确结论的序号是．

查看解析收藏纠错

+选题
17. 如图，点E，F，G分别在正方形ABCD的边AB，BC，AD上，AF⊥EG.若AB＝5，AE＝DG＝1，则BF＝.

查看解析收藏纠错

+选题
18. 学习投影后，小华利用灯光下自己的影子长度来测量一路灯的高度.如图，身高1.7m的小明从路灯灯泡A的正下方点B处，沿着平直的道路走8m到达点D处，测得影子DE长是2m，则路灯灯泡A离地面的高度AB为m.

查看解析收藏纠错

+选题

三、解答题

19. △ABC在边长为l的正方形网格中如图所示．

①以点C为位似中心，作出△ABC的位似图形△A₁B₁C，使其位似比为1：2．且△A₁B₁C位于点C的异侧，并表示出A₁的坐标．

②作出△ABC绕点C顺时针旋转90°后的图形△A₂B₂C．

③在②的条件下求出点B经过的路径长．

查看解析收藏纠错

+选题
20. 如图，利用标杆 $\text{[math]}$ 测量楼高，点A，D，B在同一直线上， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为E，C.若测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，楼高 $\text{[math]}$ 是多少？

查看解析收藏纠错

+选题
21. 如图，边长为1的正方形 $\text{[math]}$ 中，点E为 $\text{[math]}$ 的中点．连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠得到 $\text{[math]}$ 交 $\text{[math]}$ 于点G ，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
22. 如图，在平行四边形 $\text{[math]}$ 中，E为 $\text{[math]}$ 边的中点，连接 $\text{[math]}$ ，若 $\text{[math]}$ 的延长线和 $\text{[math]}$ 的延长线相交于点F.

（1）求证： $\text{[math]}$ ；

（2）连接 $\text{[math]}$ 和 $\text{[math]}$ 相交于点为G，若 $\text{[math]}$ 的面积为2，求平行四边形 $\text{[math]}$ 的面积.

查看解析收藏纠错

+选题
23. 如图，在 $\text{[math]}$ 中，点E、F分别在边 $\text{[math]}$ 、 $\text{[math]}$ 上，且 $\text{[math]}$ .

（1）探究四边形 $\text{[math]}$ 的形状，并说明理由；

（2）连接 $\text{[math]}$ ，分别交 $\text{[math]}$ 、 $\text{[math]}$ 于点G、H，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点O.若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题
24. 如图，在正方形ABCD中，点E，F分别为边BC，CD上的点，且AE⊥BF于点P，G为AD的中点，连接GP，过点P作PH⊥GP交AB于点H，连接GH.

（1）求证：BE＝CF；

（2）若AB＝6，BE $\text{[math]}$ BC，求GH的长.

查看解析收藏纠错

+选题
25. 小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形ABCD绕点A顺时针旋转α（0°＜α≤90°），得到矩形AB′C′D′，连结BD ．

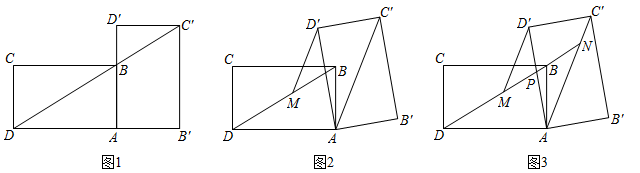
[探究1]如图1，当α＝90°时，点C′恰好在DB延长线上．若AB＝1，求BC的长．

[探究2]如图2，连结AC′，过点D′作D′M∥AC′交BD于点M ．线段D′M与DM相等吗？请说明理由．

[探究3]在探究2的条件下，射线DB分别交AD′，AC′于点P ， N（如图3），发现线段DN ， MN ， PN存在一定的数量关系，请写出这个关系式，并加以证明．

查看解析收藏纠错

+选题

湘教版数学九年级上册《 第3章 图形的相似》单元测试B卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

湘教版数学九年级上册《第3章图形的相似》单元测试B卷

相关试卷收起∨