云南省昆明市盘龙区2021年中考数学二模试卷

1. 2020年一季度，受新冠肺炎疫情影响，云南省外贸进出口总值466.5亿元，较上年同期下降6.3%.2021年一季度，云南省外贸进出口总值达742.1亿元，同比增长59.7%．若下降6.3%，记作 $\text{[math]}$ ，则增长59.7%应记作（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列标志中，既是轴对称图形，又是中心对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 如图，将木条a，b与c钉在一起， $\text{[math]}$ ，若要使木条a与b平行，则 $\text{[math]}$ 的度数应为（）

A . 40° B . 50° C . 90° D . 130°

查看解析收藏纠错

+选题
4. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 下列说法正确的是（）

A . “打开电视机，正在播放《云南新闻》”是必然事件 B . 天气预报“明天降水的概率为50%”，是指明天有一半的时间会下雨 C . 甲、乙两人在相同的条件下各射击10次，他们成绩的平均数相同，方差分别是 $\text{[math]}$ ， $\text{[math]}$ ，则甲的成绩更稳定 D . 为了了解一批灯泡的使用寿命，应采用全面调查的方式

查看解析收藏纠错

+选题
6. 定义运算： $\text{[math]}$ .例如 $\text{[math]}$ .则方程 $\text{[math]}$ 的根的情况为（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 无实数根 D . 只有一个实数根

查看解析收藏纠错

+选题
7. 已知，如图，正方形 $\text{[math]}$ 的面积为25，菱形 $\text{[math]}$ 的面积为20，求阴影部分的面积（）

A . 11 B . 6.5 C . 7 D . 7.5

查看解析收藏纠错

+选题
8. 如图，在平面直角坐标系中 $\text{[math]}$ 条直线为 $\text{[math]}$ ，直线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，直线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线交 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称，抛物线 $\text{[math]}$ 过 $\text{[math]}$ 三点，下列判断中：① $\text{[math]}$ ；② $\text{[math]}$ ；③抛物线关于直线 $\text{[math]}$ 对称；④抛物线过点 $\text{[math]}$ ；⑤四边形 $\text{[math]}$ ，其中正确的个数有（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

9. -3的绝对值等于。

查看解析收藏纠错

+选题
10. 极不平凡的2020年，云南统筹推进疫情防控和经济社会发展，在大战大考中交出优异答卷.2021年初，云南高速公路通车里程超过9000公里，跃居全国第二．数据9000用科学记数法表示为．

查看解析收藏纠错

+选题
11. 如图，观察图中的尺规作图痕迹，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
12. 若实数a，b满足 $\text{[math]}$ ，则因式分解 $\text{[math]}$ ．

查看解析收藏纠错

+选题
13. 如图，如果一只蚂蚁从圆锥底面上的点B出发，沿表面爬到母线AC的中点D处，则最短路线长为．

查看解析收藏纠错

+选题
14. 如图，在矩形 $\text{[math]}$ 中，点E是 $\text{[math]}$ 的中点，点F为射线 $\text{[math]}$ 上的一个动点， $\text{[math]}$ 沿着 $\text{[math]}$ 折叠得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，分别交 $\text{[math]}$ 和 $\text{[math]}$ 于点N和M，已知 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 与 $\text{[math]}$ 相似，则 $\text{[math]}$ 的长是．

查看解析收藏纠错

+选题

15. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
16. 如图，已知 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ．

查看解析收藏纠错

+选题

17. 2021年4月15日，是国家安全法颁布实施以来的第六个全民国家安全教育日．为了普及国家安全知识，提高维护国家安全意识，我市举办了国家安全保密知识竞赛．某校初一、初二、初三年级分别有学生300人，现从各年级中分别随机抽取20名学生的测试成绩（百分制，成绩均为整数），并对数据（成绩）进行了整理、描述和分析．下面给出了部分信息：

（ⅰ）初一年级测试成绩的频数分布表如下（不完整）：

初一年级测试成绩频数分布表

分组/分	频数	频率
$\text{[math]}$	2	0.1
$\text{[math]}$	2	0.1
$\text{[math]}$	$\text{[math]}$	0.2
$\text{[math]}$	12	$\text{[math]}$
合计	20	1.0

（ⅱ）初二年级测试成绩的频数分布直方图如下：

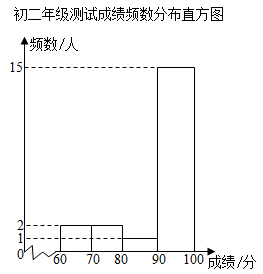
其中初二年级测试成绩在“ $\text{[math]}$ ”这一组的数据是：

95 100 96 99 98 98 99 97 99 100 100 99 100 95 100

（ⅲ）初三年级测试成绩的扇形统计图如下：

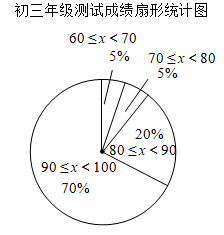
（ⅳ）初一、初二、初三年级测试成绩的平均数、众数、中位数和满分率如下（不完整）：

年级	平均数	众数	中位数	满分率
初一	90	100	93	20%
初二	93	100	$\text{[math]}$	$\text{[math]}$
初三	92	99	96.5	10%

（说明：成绩90分及以上为优秀，80~89分为良好，60~79分为合格，60分以下为不合格）根据以上信息，回答下列问题：

（1）在上述统计图表中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；

（2）初三年级测试成绩扇形统计图中“ $\text{[math]}$ ”部分所对的圆心角是度；

（3）根据以上数据分析：你认为哪个年级的竞赛成绩较好，并说明理由（至少从两个不同的角度说明推断的合理性）

查看解析收藏纠错

+选题

18. 观察以下等式：
第1个等式： $\text{[math]}$

第 $\text{[math]}$ 个等式： $\text{[math]}$

第3个等式： $\text{[math]}$

第 $\text{[math]}$ 个等式： $\text{[math]}$

第5个等式： $\text{[math]}$

······

按照以上规律．解决下列问题：

（1）写出第6个等式；

（2）写出你猜想的第n个等式：(用含n的等式表示)，并证明．

查看解析收藏纠错

+选题
19. 甲、乙两人玩摸牌游戏，把同一副扑克牌中的红桃1，2，3有数字的一面朝下放置，洗匀后甲先抽取一张，记下数字后将牌放回，洗匀后乙再抽取一张．设甲、乙两人抽到的牌面数字分别为x和y．

（1）请用列表法或树状图法（树状图也称树形图）中的一种方法，求 $\text{[math]}$ 所有可能出现的结果；

（2）求甲、乙两人摸到的牌面数字组成的点 $\text{[math]}$ 落在反比例函数 $\text{[math]}$ 图象上的概率．

查看解析收藏纠错

+选题
20. 如图，已知点E是 $\text{[math]}$ 中 $\text{[math]}$ 边的中点，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于点F，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

（1）求证：四边形 $\text{[math]}$ 为矩形；

（2）若 $\text{[math]}$ 是等边三角形，且边长为4，求四边形 $\text{[math]}$ 的面积．

查看解析收藏纠错

+选题
21. 某校喜迎中华人民共和国成立70周年，将举行以“歌唱祖国”为主题的歌咏比赛.需要在文具店购买国旗图案贴纸和小红旗发给学生做演出道具。已知每袋贴纸有50张.每袋小红旗有20面，贴纸和小红旗需整袋购买.每袋贴纸价格比每袋小红旗价格少5元.用150元购买贴纸所得袋数与用200元购买小红旗所得袋数相同.

（1）求每袋国旗图案贴纸和每袋小红旗的价格各是多少元?

（2）如果给每位演出学生分发国旗图案贴纸2张.小红旗1面.设购买国旗图案贴纸a袋(a为正整数).则购买小红旗多少袋能恰好配套?请用含a的代数式表示.

（3）在文具店累计购物超过800元后，超出800元的部分可享受8折优惠.学校按(2)中的配套方案购买，共支付w元.求w关于a的函数关系式.现全校有1200名学生参加演出，需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?

查看解析收藏纠错

+选题
22. 如图，以 $\text{[math]}$ 为直径作 $\text{[math]}$ ，过点A作 $\text{[math]}$ 的切线 $\text{[math]}$ ，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点D，点E是 $\text{[math]}$ 边的中点，连结 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
23. 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，点M为抛物线的顶点，点B在y轴上，且 $\text{[math]}$ ，直线 $\text{[math]}$ 与抛物线在第一象限交于点 $\text{[math]}$ ．

（1）求抛物线的解析式及顶点M的坐标；

（2）求直线 $\text{[math]}$ 的函数解析式及 $\text{[math]}$ 的值；

（3）连接 $\text{[math]}$ ，若过点O的直线交线段 $\text{[math]}$ 于点P，将 $\text{[math]}$ 的面积分成1：2的两部分，请求出点P的坐标；

（4）在坐标平面内是否存在点N，使以点A、O、C、N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题

云南省昆明市盘龙区2021年中考数学二模试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

云南省昆明市盘龙区2021年中考数学二模试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨