江苏省淮安市2021年中考数学仿真模拟试卷

修改时间：2021-05-31 浏览次数：226 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 如果a与3互为相反数，则 $\text{[math]}$ 是（）

A . 3 B . ﹣3 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列各运算中，计算正确的是（）

A . x³+2x³=3x⁶ B . (x³)³=x⁶ C . x³·x⁹=x¹² D . x³÷x =x⁴

查看解析收藏纠错

+选题
3. 如图所示的几何体的左视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 一个多边形外角和是内角和的2倍，这个多边形是（）

A . 三角形 B . 四边形 C . 六边形 D . 不能确定

查看解析收藏纠错

+选题
5. 点A（3，﹣1）关于原点的对称点A′的坐标是（　　）

A . （﹣3，﹣1） B . （3，1） C . （﹣3，1） D . （﹣1，3）

查看解析收藏纠错

+选题
6. 2015年某中学举行的春季田径运动会上，参加男子跳高的15名运动员的成绩如表所示：
成绩（m）
1.80
1.50
1.60
1.65
1.70
1.75
人数
1
2
4
3
3
2
这些运动员跳高成绩的中位数和众数分别是（）

A . 1.70m，1.65m B . 1.70m，1.70m C . 1.65m，1.60m D . 3，4

查看解析收藏纠错

+选题
7. 如图， $\text{[math]}$ 均 $\text{[math]}$ 为直径，点 $\text{[math]}$ 是圆上两点，且 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

8. 计算机中常用的十六进制是逢16进1的计数制，采用数字0~9和字母A~F共16个计数符号，这些符号与十进制的数的对应关系如下表：

十六进制	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
十进制	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

例如，十进制中 $\text{[math]}$ ，用十六进制表示为1A：用十六进制表示： $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ，用 $\text{[math]}$ 十六进制可表示为（）

A . 8C B . 140 C . 32 D . EO

查看解析收藏纠错

+选题

二、填空题

9. 分解因式：4m²﹣9n²=．

查看解析收藏纠错

+选题
10. 第五届“中国数字阅读大会”在杭州举办，大会发布的《2018中国数字阅读白皮书》显示：截止2018年，我国数字阅读用户总量达到43200万人，将数据43200用科学记数法表示为．

查看解析收藏纠错

+选题
11. 数据1，2，3，a的平均数是3，数据4，5，a，b的众数是5，则a+b=．

查看解析收藏纠错

+选题
12. 分式方程 $\text{[math]}$ 的解为．

查看解析收藏纠错

+选题
13. 如图，在菱形ABCD中，AC与BD相交于O，P是AB上一点，PO＝PA＝3，则菱形ABCD的周长是．

查看解析收藏纠错

+选题
14. 菱形周长为40 cm，它的一条对角线长12 cm，则菱形的面积为cm²

查看解析收藏纠错

+选题
15. 顶点为P的抛物线 $\text{[math]}$ 与y轴交于Q ，则PQ的长为．

查看解析收藏纠错

+选题
16. 如图，已知菱形 $\text{[math]}$ 的对角线相交于坐标原点O，四个顶点分别在双曲线 $\text{[math]}$ 和 $\text{[math]}$ 上， $\text{[math]}$ .平行于x轴的直线与两双曲线分别交于点E，F，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积为.

查看解析收藏纠错

+选题

三、解答题

17.

（1）计算 $\text{[math]}$

（2）化简： $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

查看解析收藏纠错

+选题
18. 阅读下面的材料：
对于实数 $\text{[math]}$ ，我们定义符号 $\text{[math]}$ 的意义为：当 $\text{[math]}$ 时， $\text{[math]}$ ；当 $\text{[math]}$ 时， $\text{[math]}$ ，如： $\text{[math]}$ ．

根据上面的材料回答下列问题：

（1） $\text{[math]}$ ；

（2）当 $\text{[math]}$ 时，求x的取值范围．

查看解析收藏纠错

+选题
19.
某校九（2）班40名同学为“希望工程”捐款，共捐款400元，捐款情况如下表：表格中捐款10元和15元的人数不小心被墨水污染已看不清楚．捐款10元和15元的人数各是多少名？

捐款（元）

5

10

15

20

人数

12

3

查看解析收藏纠错

+选题
20. 如图1，在▱ABCD中，对角线AC与BD相交于点O，经过点O的直线与边AB相交于点E，与边CD相交于点F．

（1）求证：OE=OF；

（2）如图2，连接DE，BF，当DE⊥AB时，在不添加其他辅助线的情况下，直接写出腰长等于 $\text{[math]}$ BD的所有的等腰三角形．

查看解析收藏纠错

+选题
21. 为了调查疫情对青少年人生观、价值观产生的影响，轩宁中学团委对部分学生进行了问卷调查，其中一项是：疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图（不完整）如图所示，请你根据图中提供的信息回答下列问题：

（1）本次调查共抽取了多少名学生?

（2）通过计算补全条形统计图；

（3）若轩宁中学共有 $\text{[math]}$ 名学生，请你估计该中学选择“生命”词汇的学生有多少名?

查看解析收藏纠错

+选题
22. 现如今，“垃圾分类”意识已深入人心，如图是生活中的四个不同的垃圾投放桶，分别写着：有害垃圾、厨余垃圾、其他垃圾、可回收垃圾．其中小明投放了一袋垃圾，小丽投放了两袋垃圾．

（1）写出小明投放的垃圾恰好是“厨余垃圾”的概率；

（2）用列表法或画树状图法求小丽投放的两袋垃圾是不同类的概率

查看解析收藏纠错

+选题
23.
“低碳环保，你我同行”．两年来，绍兴市区的公共自行车给市民出行带来切实方便．如图1所示是一辆自行车的实物图．车架档AC与CD的长分别为45cm，60cm，且它们互相垂直，座杆CE的长为20cm，点A，C，E在同一条直线上，且∠CAB=75°，如图2，图3是公共自行车车桩的截面示意图，PQ⊥PM，PM⊥MN，点Q，N在GO上，GO∥HF，PQ=80cm，PM=24cm，QN=25cm，GH=4cm.

（1）求车架档AD的长；

（2）求车座点E到车架档AB的距离及车桩的截面示意图中的点P到地面的距离．
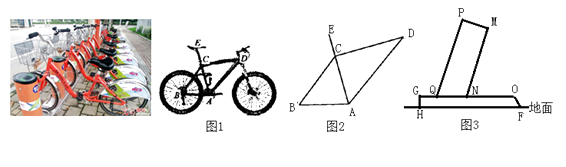
（结果精确到1cm．参考数据：sin75°≈0.97，cos75°≈0.26，tan75≈3.73）

查看解析收藏纠错

+选题
24. 如图①，一个正方体铁块放置在圆柱形水槽内，现以一定的速度往水槽中注水，28s时注满水槽．水槽内水面的高度y（cm）与注水时间x（s）之间的函数图象如图②所示．

（1）正方体的棱长为cm；

（2）求线段AB对应的函数解析式，并写出自变量x的取值范围；

（3）如果将正方体铁块取出，又经过t（s）恰好将此水槽注满，直接写出t的值．

查看解析收藏纠错

+选题
25. 如图，△ABC内接于⊙O，且∠B=60°，过C作⊙O的切线l，与直径AD的延长线交于点E，AF⊥l，垂足为F．

（1）求证：AC平分∠FAD；

（2）已知AF=3 $\text{[math]}$ ，求阴影部分面积．

查看解析收藏纠错

+选题
26.

（1）问题发现

如图1，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝50°，连接BD，CE交于点F.填空：

①的值为；②∠BFC的度数为.

（2）类比探究
如图2，在矩形ABCD和△DEF中，AD＝ $\text{[math]}$ AB，∠EDF＝90°，∠DEF＝60°，连接AF交CE的延长线于点P.求 $\text{[math]}$ 的值及∠APC的度数，并说明理由；

（3）拓展延伸
在（2）的条件下，将△DEF绕点D在平面内旋装，AF，CE所在直线交于点P，若DF＝ $\text{[math]}$ ，AB＝ $\text{[math]}$ ，求出当点P与点E重合时AF的长.

查看解析收藏纠错

+选题
27. 如图，抛物线y＝﹣x²+bx+c与x轴交于A、B两点，与y轴交于点C ．直线y＝x﹣5经过点B、C ．

（1）求抛物线的解析；

（2）点P是直线BC上方抛物线上一动点，连接PB、PC ．
①当△PBC的面积最大时，求点P的坐标；

②在①的条件下，y轴上存在点M ，使四边形PMAB的周长最小，请求出点M的坐标；

③连接AC ，当tan∠PBO＝2tan∠ACO时，请直接写出点P的坐标．

查看解析收藏纠错

+选题

成绩（m）	1.80	1.50	1.60	1.65	1.70	1.75
人数	1	2	4	3	3	2

捐款（元）	5	10	15	20
人数	12			3

江苏省淮安市2021年中考数学仿真模拟试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨