2021年河南省中考数学线上公益大模考诊断试卷

修改时间：2021-06-19 浏览次数：188 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. ﹣ $\text{[math]}$ 的绝对值是（）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . ﹣5 D . 5

查看解析收藏纠错

+选题
2. 2020年，我国国内生产总值达到101.6万亿元，数据“101.6万亿”用科学记数法表示为（）

A . 10.16×10¹³ B . 0.1016×10¹⁵ C . 1.016×10¹² D . 1.016×10¹⁴

查看解析收藏纠错

+选题
3. 将一块直角三角尺ABC按如图所示的方式放置，其中点A、C分别落在直线a、b上，若a∥b，∠1＝65°，则∠2的度数为（）

A . 75° B . 65° C . 35° D . 25°

查看解析收藏纠错

+选题
4. 下列计算正确的是（）

A . a²+a³＝a⁵ B . （﹣2a）³＝﹣6a³ C . a³•a⁵＝a⁸ D . （a﹣2）²＝a²﹣4

查看解析收藏纠错

+选题
5. 如图是由7个相同的小正方体搭成的几何体，在标号为①的小正方体上方添加一个小正方体后，所得几何体的三视图与原几何体的三视图相比没有发生变化的是（）

A . 主视图和俯视图 B . 主视图和左视图 C . 左视图和俯视图 D . 主视图、左视图和俯视图

查看解析收藏纠错

+选题
6. 若点A（﹣2，y₁），B（﹣1，y₂）在反比例函数y＝ $\text{[math]}$ 的图象上，则y₁﹣y₂的值为（）

A . 负数 B . 0 C . 正数 D . 无法确定

查看解析收藏纠错

+选题
7. 下列说法正确的是（）

A . 了解河南省初中生身高情况适宜全面调查 B . 甲，乙两名射击运动员5次射击成绩的方差分别为s_甲²＝1.2，s_乙²＝2，说明甲的射击成绩比乙的射击成绩稳定 C . 同旁内角互补是必然事件 D . 已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次

查看解析收藏纠错

+选题
8. 关于x的一元二次方程x（x+1）﹣3＝mx的根的情况是（）

A . 无实数根 B . 有两个相等的实数根 C . 有两个不相等的实数根 D . 无法判断

查看解析收藏纠错

+选题
9. 如图，在▱ABCD中，AB＝2 $\text{[math]}$ ，点E为AD的中点，按以下步骤作图：①以点E为圆心，EA长为半径作弧，交AB于点F；②再分别以点A和点F为圆心，大于 $\text{[math]}$ AF的长为半径作弧，两弧相交于点M；③作直线EM交AB于点N，连接CE.若∠ADC＝135°，DE＝2，则CE的长为（）

A . 2 $\text{[math]}$ B . 4 $\text{[math]}$ C . 2 $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，在正方形ABCD中，顶点A，B，C，D在坐标轴上，且B（4，0），以AB为边构造菱形ABEF，将菱形ABEF与正方形ABCD组成的图形绕点O顺时针旋转，每次旋转45°，则第164次旋转结束时，点 $\text{[math]}$ 的坐标为（）

A . （﹣4，4 $\text{[math]}$ ） B . （﹣4，﹣4 $\text{[math]}$ ） C . （4 $\text{[math]}$ ，﹣4） D . （﹣4 $\text{[math]}$ ，﹣4）

查看解析收藏纠错

+选题

二、填空题

11. 若 $\text{[math]}$ 都是无理数，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值分别是（填一组满足条件的值）.

查看解析收藏纠错

+选题
12. 关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 的解集在数轴上如图表示，则 $\text{[math]}$ 的值为.

查看解析收藏纠错

+选题
13. 某社团中有三名男生和一名女生，该社团将随机选派两名同学作为代表参加市级比赛，恰好选中一男一女的概率是.

查看解析收藏纠错

+选题
14. 如图，在扇形BCD中，∠BCD＝150°，以点B为圆心，BC长为半径画弧交 $\text{[math]}$ 于点A，连接AC，若BC＝4，则图中阴影部分的面积为.

查看解析收藏纠错

+选题
15. 如图，在矩形ABCD中，AB＝6，AD＝8，E、F分别为AB、CD边上的点，且EF∥BC，G为EF上一点，且GF＝2，M、N分别为GD、EC的中点，则MN＝.

查看解析收藏纠错

+选题

三、解答题

16. 先化简，再求值：（ $\text{[math]}$ ﹣1）÷ $\text{[math]}$ ，其中a＝ $\text{[math]}$ +2.

查看解析收藏纠错

+选题

17. 某校为了解七、八年级学生对“文明知识礼仪”的掌握情况，从七、八年级各随机抽取了25名学生进行相关测试，并对成绩进行整理、描述和分析，部分信息如下：

c.八年级D组测试成绩数据为：90，90，91，92，93，94，94；

d.七、八年级被抽取学生测试成绩的平均数、中位数如下表所示：

	平均数	中位数
七年级	87.36	87
八年级	91.36	a

根据所给信息，解答下列问题：

（1）根据统计图，对比两个年级成绩在90分以上（含90分）的百分比，七年级比八年级；（填“大”或“小”）

（2）表中a的值为；

（3）小华的测试成绩为89分，他的成绩在本年级参加测试的学生中处于中上游，请判断小华是 ▲ 年级的学生，并说明理由；

（4）学校决定对本次测试成绩优异的学生进行奖励，老师从七、八年级各抽取了4名同学的成绩记录如下表：

	七年级				八年级
学生代码	A	B	C	D	E	F	G	H
成绩	98	93	90	95	87	96

其中有两名同学的成绩被墨汁污染了，但老师说七年级和八年级被抽取的这4名同学中各有2名同学可以获得奖励，于是小明说G和H两名同学中只有一名同学可以获得奖励.请问小明的说法是否正确？并说明理由.

查看解析收藏纠错

+选题

18. 蔡明园公园位于河南省驻马店市上蔡县蔡都镇西南部，其公园南山门被誉为“亚洲第一门”，学完了三角函数知识后，某数学“综合与实践”小组的同学把“测量南山门最高点的高度”作为一项课题活动，他们制定了测量方案，并利用课余时间完成了实地测量.为了减小测量误差，小组在测量仰角以及两点间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如表：

课题	测量南山门最高点的高度
实物图
成员	组长：xxx 组员：xxx，xxx，xxx
测量工具	卷尺、测角仪……
测量示意图				说明：AB表示南山门最高点到地面的竖直距离.测角仪的高度CD-EF-1.5m点C.F与点B在同一直线上，点C.F之间的距离可直接测将，且点A、B.C.D.E、F在同一平面内.
测量数据	第一次	第二次	平均值
	35.95°	36.05°	36°
	45.09°	44.91°	45°
	79.58m	79.62m	79.6m
……	……

（1）请帮助该小组的同学根据上表中的测量数据，求南山门最高点的高度AB.（结果精确到0.1m，参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73， $\text{[math]}$ ≈1.41）

（2）该小组要写出一份完整的课题活动报告，除上表中的项目外，你认为还需要补充哪些项目？（写出一个即可）（如需作图或作辅助线，请先将原题草图画在对应题目的答题区域后再作答.）

查看解析收藏纠错

+选题

19. 为提升校园体育运动多样性，助力师生“阳光运动”，某校决定采购一批排球和足球，小明在某体育用品商店咨询了排球和足球的售价具体信息：购买2个排球和3个足球共需460元，购买12个排球所需费用与购买5个足球所需费用相同.

（1）求排球和足球的售价分别是多少元？

（2）若该校计划购进排球和足球共100个，其中排球的数量不超过足球的3倍，请设计出最省钱的购买方案，并说明理由.

查看解析收藏纠错

+选题
20. 如图，抛物线y＝ax²﹣4x+c经过点A（2，﹣2），且当x＝1时，函数y有最小值.（如需作图或作辅助线，请先将原题草图画在对应题目的答题区域后再作答.）

（1）求抛物线的解析式；

（2）点B的坐标为（﹣3，﹣4），点B关于原点的对称点为B'，点C是抛物线对称轴上一动点，若抛物线在直线BB'下方的部分与直线BC有公共点，求点C纵坐标y_c的取值范围.

查看解析收藏纠错

+选题
21. 若一直线与圆相交，过交点作圆的切线，则此切线与直线的交角中的任意一个称为直线和圆的交角，其中所夹弧为劣弧的角为劣交角，所夹弧为优弧的角为优交角.直线和圆的交角有以下性质：直线和圆的交角等于所夹弧所对的圆周角.（如需作图或作辅助线，请先将原题草图画在对应题目的答题区域后再作答.）

（1）为了说明直线和圆的交角性质的正确性，需要对其进行证明.如下给出了不完整的“已知”和“求证”，请补充完整，并写出“证明”过程（只证明劣交角即可）.
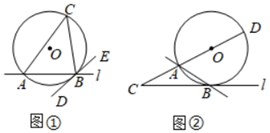
已知：如图①，直线l与⊙O相交于点A、B，过点B作.

求证：∠ABD＝.

（2）如图②，直线l与⊙O相交于点A、B，AD为⊙O的直径，BC切⊙O于点B，交DA的延长线于点C，若AD＝BC，AC＝2，求⊙O的半径.

查看解析收藏纠错

+选题
22. 如图①，在△ABC中，∠ACB＝90°，AC＝BC，AB＝6cm，E是线段AB上一动点，D是BC的中点，过点C作射线CG，使CG∥AB，连接ED并延长交CG于点F，连接AF.设A、E两点间的距离为xcm，E、F两点间的距离为ycm.小亮根据学习函数的经验，对因变量y随自变量x变化而变化的规律进行了探究.（如需作图或作辅助线，请先将原题草图画在对应题目的答题区域后再作答.）下面是小亮的探究过程，请补充完整：

（1）列表：如表的已知数据是根据A、E两点间的距离x进行取点、画图、测量，分别得到了x与y的几组对应值：

x/cm

0

1

2

3

4

5

6

y/cm

9.49

7.62

5.83

3.16

3.16

4.24

请你通过计算补全表格；

（2）描点、连线：在平面直角坐标系xOy中，描出剩余的点（x，y），并画出函数y关于x的图象；

（3）根据函数图象，当E、F两点间的距离y最小时，A、E两点间的距离约为cm；

（4）解决问题：当EF﹣AE＝2时，BE的长度大约是cm.（结果保留1位小数）

查看解析收藏纠错

+选题
23. 如图①，△ABC为直角三角形，∠ACB＝90°，∠BAC＝30°，点D在AB边上，过点D作DE⊥AC于点E，取BC边的中点F，连接DF并延长到点G，使FG＝DF，连接CG.（如需作图或作辅助线，请先将原题草图画在对应题目的答题区域后再作答.）

（1）问题发现：
填空：CE与CG的数量关系是，直线CE与CG所夹的锐角的度数为.

（2）探究证明：
将△ADE绕点A逆时针旋转，（1）中的结论是否仍然成立，若成立，请仅就图②所示情况给出证明，若不成立，请说明理由；

（3）问题解决：
若AB＝4，AD＝3，将△ADE由图①位置绕点A逆时针旋转α（0°＜α＜180°），当△ACE是直角三角形时，请直接写出CG的值.

查看解析收藏纠错

+选题

x/cm	0	1	2	3	4	5	6
y/cm	9.49	7.62	5.83		3.16	3.16	4.24

2021年河南省中考数学线上公益大模考诊断试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨