修改时间:2021-05-25 浏览次数:156 类型:三轮冲刺
车型号 | 每辆车的座位数 | 每辆车每天的租金(元) |
A | 10 | 500 |
B | 20 | 900 |
C | 30 | 1250 |
(1)设租用A型车x辆,B型车y辆.求y与x之间的函数解析式;
(2)设每天租金的总金额为z元.求出z与x之间函数解析式;
(3)你能为华丰电子厂提出租车的方案吗?如能,最多可以提出多少个方案?其中每天租金最少的方案是什么?(要求:提出的方案应符合题目要求,并要有数学依据;其中每天租金最少方案结论中应明确租用A、B、C三种型号的车各多少辆,这时每天租金是多少.)
一位数学老师参加本市自来水价格听证会后,编写了一道应用题,题目如下:节约用水、保护水资源,是科学发展观的重要体现.依据这种理念,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系.
请你解答下列问题:
(1)将m看作已知量,分别写出当0<x<m和x>m时,y与x之间的函数关系式;
(2)按上述方案,一家酒店四、五两月用水量及缴费情况如下表所示,那么,这家酒店四、五两月的水费分别是按哪种方案计算的?并求出m的值.
| 月份 | 用水量x(吨) | 水费y(元) |
| 四月 | 35 | 59.5 |
| 五月 | 80 | 151 |

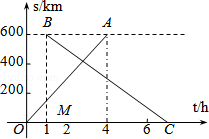
①求第二列动车组列车出发多长时间后与普通快车相遇?
②请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔.
按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(a)新数据都在60~100(含60和100)之间;
(b)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。
(1)若y与x的关系是y=x+p(100-x),请说明:当p=时,这种变换满足上述两个要求;
(2)若按关系式y=a(x-h)2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式。(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)
(1)反比例函数y=是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y=x2﹣2x﹣k是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
试题篮