2016年湖北省襄阳市中考数学试卷

1. ﹣3的相反数是（　　）

A . 3 B . ﹣3 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
2.
如图，AD是∠EAC的平分线，AD∥BC，∠B=30°，则∠C的度数为（　　）

A . 50° B . 40° C . 30° D . 20°

查看解析收藏纠错

+选题
3. ﹣8的立方根是（　　）

A . 2 B . ﹣2 C . ±2 D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
4.
一个几何体的三视图如图所示，则这个几何体是（　　）

A . 球体 B . 圆锥 C . 棱柱 D . 圆柱

查看解析收藏纠错

+选题
5. 不等式组 $\text{[math]}$ 的整数解的个数为（　　）

A . 0个 B . 2个 C . 3个 D . 无数个

查看解析收藏纠错

+选题
6. 一组数据2，x，4，3，3的平均数是3，则这组数据的中位数、众数、方差分别是（　　）

A . 3，3，0.4 B . 2，3，2 C . 3，2，0.4 D . 3，3，2

查看解析收藏纠错

+选题
7.
如图，在▱ABCD中，AB＞AD，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于 $\text{[math]}$ EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论中不能由条件推理得出的是（　　）

A . AG平分∠DAB B . AD=DH C . DH=BC D . CH=DH

查看解析收藏纠错

+选题
8.
如图，I是△ABC的内心，AI的延长线和△ABC的外接圆相交于点D，连接BI、BD、DC．下列说法中错误的一项是（　　）

A . 线段DB绕点D顺时针旋转一定能与线段DC重合 B . 线段DB绕点D顺时针旋转一定能与线段DI重合 C . ∠CAD绕点A顺时针旋转一定能与∠DAB重合 D . 线段ID绕点I顺时针旋转一定能与线段IB重合

查看解析收藏纠错

+选题
9.
如图，△ABC的顶点是正方形网格的格点，则sinA的值为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10.
一次函数y=ax+b和反比例函数y= $\text{[math]}$ 在同一平面直角坐标系中的图象如图所示，则二次函数y=ax²+bx+c的图象大致为（　　）

A . B . C . D .

查看解析收藏纠错

+选题

11. 分解因式：2a²﹣2=．

查看解析收藏纠错

+选题
12. 关于x的一元二次方程x²﹣2x+m﹣1=0有两个相等的实数根，则m的值为．

查看解析收藏纠错

+选题
13. 一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球．每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中约有红球个．

查看解析收藏纠错

+选题
14. 王经理到襄阳出差带回襄阳特产﹣﹣孔明菜若干袋，分给朋友们品尝，如果每人分5袋，还余3袋；如果每人分6袋，还差3袋，则王经理带回孔明菜袋．

查看解析收藏纠错

+选题
15.
如图，AB是半圆O的直径，点C、D是半圆O的三等分点，若弦CD=2，则图中阴影部分的面积为．

查看解析收藏纠错

+选题
16.
如图，正方形ABCD的边长为2 $\text{[math]}$ ，对角线AC、BD相交于点O，E是OC的中点，连接BE，过点A作AM⊥BE于点M，交BD于点F，则FM的长为

查看解析收藏纠错

+选题

17. 先化简，再求值：（2x+1）（2x﹣1）﹣（x+1）（3x﹣2），其中x= $\text{[math]}$ ．

查看解析收藏纠错

+选题
18.
襄阳市文化底蕴深厚，旅游资源丰富，古隆中、习家池、鹿门寺三个景区是人们节假日玩的热点景区，张老师对八（1）班学生“五•一”小长假随父母到这三个景区游玩的计划做了全面调查，调查分四个类别：A、游三个景区；B、游两个景区；C、游一个景区；D、不到这三个景区游玩．现根据调查结果绘制了不完整的条形统计图和扇形统计图，请结合图中信息解答下列问题：

（1）八（1）班共有学生人，在扇形统计图中，表示“B类别”的扇形的圆心角的度数为；

（2）请将条形统计图补充完整；

（3）若张华、李刚两名同学，各自从三个景区中随机选一个作为5月1日游玩的景区，则他们同时选中古隆中的概率为．

查看解析收藏纠错

+选题
19.
如图，在△ABC中，AD平分∠BAC，且BD=CD，DE⊥AB于点E，DF⊥AC于点F．

（1）求证：AB=AC；

（2）若AD=2 $\text{[math]}$ ，∠DAC=30°，求AC的长．

查看解析收藏纠错

+选题
20.
如图，直线y=ax+b与反比例函数y= $\text{[math]}$ （x＞0）的图象交于A（1，4），B（4，n）两点，与x轴、y轴分别交于C、D两点．

（1） m=，n=；若M（x₁ ， y₁），N（x₂ ， y₂）是反比例函数图象上两点，且0＜x₁＜x₂ ，则y₁y₂（填“＜”或“=”或“＞”）；

（2）若线段CD上的点P到x轴、y轴的距离相等，求点P的坐标．

查看解析收藏纠错

+选题
21. “汉十”高速铁路襄阳段正在建设中，甲、乙两个工程队计划参与一项工程建设，甲队单独施工30天完成该项工程的 $\text{[math]}$ ，这时乙队加入，两队还需同时施工15天，才能完成该项工程．

（1）若乙队单独施工，需要多少天才能完成该项工程？

（2）若甲队参与该项工程施工的时间不超过36天，则乙队至少施工多少天才能完成该项工程？

查看解析收藏纠错

+选题
22.
如图，直线AB经过⊙O上的点C，直线AO与⊙O交于点E和点D，OB与⊙O交于点F，连接DF、DC．已知OA=OB，CA=CB，DE=10，DF=6．

（1）求证：①直线AB是⊙O的切线；②∠FDC=∠EDC；

（2）求CD的长．

查看解析收藏纠错

+选题
23. 襄阳市某企业积极响应政府“创新发展”的号召，研发了一种新产品．已知研发、生产这种产品的成本为30元/件，且年销售量y（万件）关于售价x（元/件）的函数解析式为：y= $\text{[math]}$ ．

（1）若企业销售该产品获得的年利润为W（万元），请直接写出年利润W（万元）关于售价x（元/件）的函数解析式；

（2）当该产品的售价x（元/件）为多少时，企业销售该产品获得的年利润最大？最大年利润是多少？

（3）若企业销售该产品的年利润不少于750万元，试确定该产品的售价x（元/件）的取值范围．

查看解析收藏纠错

+选题
24.
如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．

（1）求证：四边形EFDG是菱形；

（2）探究线段EG、GF、AF之间的数量关系，并说明理由；

（3）若AG=6，EG=2 $\text{[math]}$ ，求BE的长．

查看解析收藏纠错

+选题
25.
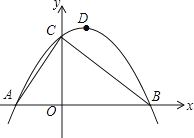
如图，已知点A的坐标为（﹣2，0），直线y=﹣ $\text{[math]}$ x+3与x轴、y轴分别交于点B和点C，连接AC，顶点为D的抛物线y=ax²+bx+c过A、B、C三点．

（1）请直接写出B、C两点的坐标，抛物线的解析式及顶点D的坐标；

（2）设抛物线的对称轴DE交线段BC于点E，P是第一象限内抛物线上一点，过点P作x轴的垂线，交线段BC于点F，若四边形DEFP为平行四边形，求点P的坐标；

（3）设点M是线段BC上的一动点，过点M作MN∥AB，交AC于点N，点Q从点B出发，以每秒1个单位长度的速度沿线段BA向点A运动，运动时间为t（秒），当t（秒）为何值时，存在△QMN为等腰直角三角形？

查看解析收藏纠错

+选题

2016年湖北省襄阳市中考数学试卷

一、选择题：

二、填空题：

三、解答题：

相关试卷收起∨

2016年湖北省襄阳市中考数学试卷

一、选择题：

二、填空题：

三、解答题：

相关试卷 收起∨

相关试卷收起∨