吉林省长春市新区2019-2020学年九年级上学期数学期末试卷

1. 下列式子中，a不可以取1和2的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 已知2x＝3y ，则下列各式错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 6x＝9y

查看解析收藏纠错

+选题
3. 下列成语所描述的事件为随机事件的是（）

A . 守株待兔 B . 水中捞月 C . 瓮中捉鳖 D . 拔苗助长

查看解析收藏纠错

+选题
4. 已知关于x的一元二次方程x²﹣x+a²﹣1＝0的一个根为0，则a的值为（）

A . 1 B . ﹣1 C . ±1 D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 用放大镜观察一个五边形时，不变的量是（）

A . 各边的长度 B . 各内角的度数 C . 五边形的周长 D . 五边形的面积

查看解析收藏纠错

+选题
6.
如图，已知直线a∥b∥c ，直线m、n与直线a、b、c分别交于点A、C、E、B、D、F ， AC=4，CE=6，BD=3，则BF=（　　）.

A . 7 B . 7.5 C . 8 D . 8.5

查看解析收藏纠错

+选题
7. 在Rt△ABC中，∠C＝90°，若a=3,b=4，则sinB的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 二次函数 $\text{[math]}$ 的图象大致是（）

A . B . C . D .

查看解析收藏纠错

+选题

9. $\text{[math]}$ ＝．

查看解析收藏纠错

+选题
10. 若关于x的一元二次方程x²﹣4x+4＝m没有实数根，则m的取值范围是．

查看解析收藏纠错

+选题
11. 抛物线y＝﹣（x﹣1）（x+3）的对称轴方程为．

查看解析收藏纠错

+选题
12. 如图，△ADE～△ABC，AD＝3，AE＝4，BE＝5，CA的长为.

查看解析收藏纠错

+选题
13. 如图，在边长为1的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点O，则cos∠AOD=．

查看解析收藏纠错

+选题
14. 一只不透明的布袋中有三种珠子（除颜色以外没有任何区别），分别是3个红珠子，4个白珠子和5个黑珠子，每次只摸出一个珠子，观察后均放回搅匀，在连续9次摸出的都是红珠子的情况下，第10次摸出红珠子的概率是.

查看解析收藏纠错

+选题

15. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
16. 四张大小、形状都相同的卡片上分别写有数字1，2，3，4，把它们放入不透明的盒子中摇匀.

（1）从中随机抽出1张卡片，抽出的卡片上的数字恰好是偶数的概率为.

（2）从中随机抽出1张卡片，记录数字后放回摇匀，再抽出一张卡片，记录数字.用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率.

查看解析收藏纠错

+选题
17. 某药品经过两次降价，每瓶零售价由56元降为31.5元．已知两次降价的百分比相同，求每次降价的百分率是多少．

查看解析收藏纠错

+选题
18. 如图，已知O是坐标原点，B、C两点的坐标分别为（3，－1）、（2，1）.

（1）以O点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出图形；

（2） B点的对应点B′的坐标是；C点的对应点C′的坐标是；

（3）在BC上有一点P（x，y），按（1）的方式得到的对应点P′的坐标是.

查看解析收藏纠错

+选题

19. 在硬地上抛掷一枚图钉，通常会出现两种情况：

下面是小明和同学做“抛掷图钉实验”获得的数据：

抛掷次数n	100	200	300	400	500	600	700	800	900	1000
针尖不着地的频数m	63	120	186	252	310	360	434	488	549	610
针尖不着地的频率 $\text{[math]}$	0.63	0.60		0.63		0.60	0.62		0.61	0.61

（1）填写表中的空格；

（2）画出该实验中，抛掷图钉钉尖不着地频率的折线统计图；

（3）根据“抛掷图钉实验”的结果，估计“钉尖着地”的概率为．

查看解析收藏纠错

+选题

20. 如图①，一台灯放置在水平桌面上，底座AB与桌面垂直，底座高AB＝5cm ，连杆BC＝CD＝20cm ， BC ， CD与AB始终在同一平面内．

（参考数据：sin37°＝0.6，cos37°＝0.8，tan37°＝0.75）

（1）如图②，转动连杆BC ， CD ，使∠BCD成平角，∠ABC＝143°，求连杆端点D离桌面l的高度DE ．

（2）将图②中的连杆CD再绕点C逆时针旋转16°，如图③，此时连杆端点D离桌面l的高度减小了cm ．

查看解析收藏纠错

+选题
21. 利用函数图象探究方程x（|x|﹣2）＝ $\text{[math]}$ 的实数根的个数．

（1）设函数y＝x（|x|﹣2），则这个函数的图象与直线y＝ $\text{[math]}$ 的交点的横坐标就是方程x（|x|﹣2）＝ $\text{[math]}$ 的实数根．

（2）分类讨论：当x≤0时，y＝﹣x²﹣2x；当x＞0时，y＝；

（3）在给定的坐标系中，已经画出了当x≤0时的函数图象，请根据（2）中的解析式，通过描点，连线，画出当x＞0时的函数图象．

（4）在给定的坐标系中画直线y＝ $\text{[math]}$ 、观察图象可知方程x（|x|﹣2）＝ $\text{[math]}$ 的实数根有个．

（5）深入探究：若关于x的方程2x（|x|﹣2）＝m有三个不相等的实数根，且这三个实数根的和为负数，则m的取值范围是．

查看解析收藏纠错

+选题
22. 已知，如图，在矩形ABCD中，AB＝8，BC＝x（0＜x≤8），点E在边CD上，且CE＝CB ，以AE为对角线作正方形AGEF ．设正方形AGEF的面积y ．

（1）当点F在矩形ABCD的边上时，x＝．

（2）求y与x的函数关系式及y的取值范围．

（3）当矩形ABCD的一条边将正方形AGEF的面积分为1：3两部分时，直接写出x的值．

查看解析收藏纠错

+选题
23. （知识回顾）
我们把连结三角形两边中点的线段叫做三角形的中位线，并且有：三角形的中位线平行于第三边，并且等于第三边的一半．

（1）（定理证明）
将下列的定理证明补充完整：

已知：如图①，在△ABC中，点D、E分别是边AB、AC中点，连结DE ．

求证：

证明：

（2）（定理应用）
如图②，在△ABC中，AB＝10，∠ABC＝60°，点P、Q分别是边AC、BC的中点，连结PQ ．

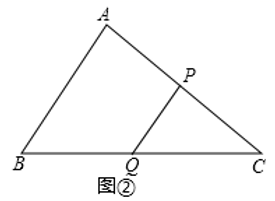
线段PQ的长为．

（3）以点C为一个端点作线段CD（CD与AB不平行），连结AD ，取AD的中点M ，连结PM、QM ．
①在图②中补全图形．

②当∠PQM＝∠PMQ时，求CD的长．

③在②的条件下，当△PQM面积最大时，直接写出∠BCD的度数．

查看解析收藏纠错

+选题
24. 如图，在平面直角坐标系中，线段AB的端点坐标分别为A（0，6）、B（6，6）．点Q在线段AB上，以Q为顶点的抛物线y＝﹣ $\text{[math]}$ x²+bx+c与y轴交于点D ，与x轴的一个交点为C ．设点Q的横坐标为m ，点C的横坐标为n（n＞m）．

（1）当m＝0时，求n的值．

（2）求线段AD的长（用含m的式子表示）；

（3）点P（2，0）在x轴上，设△BPD的面积为S ，求S与m的关系式；

（4）当△DCQ是以QC为直角边的直角三角形时，直接写出m的值．

查看解析收藏纠错

+选题

吉林省长春市新区2019-2020学年九年级上学期数学期末试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

吉林省长春市新区2019-2020学年九年级上学期数学期末试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨