江苏省扬州市广陵区2020年数学中考模拟试卷

修改时间：2024-07-13 浏览次数：221 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. －2的倒数是（）

A . － $\text{[math]}$ B . $\text{[math]}$ C . ±2 D . 2

查看解析收藏纠错

+选题
2. 函数y＝ $\text{[math]}$ 中自变量x的取值范围是（）

A . x＞2 B . x≤2 C . x≥2 D . x≠2

查看解析收藏纠错

+选题
3. 下列计算正确的是（）

A . 2a＋3b＝5ab B . (a－b)²＝a²－b² C . (2x²)³＝6x⁶ D . x⁸÷x³＝x⁵

查看解析收藏纠错

+选题
4. 下列水平放置的四个几何体中，主视图与其它三个不相同的是（　　）

A . B . C . D .

查看解析收藏纠错

+选题
5. 已知正多边形的一个内角是140°，则这个正多边形的边数是（）

A . 九边形 B . 八边形 C . 七边形 D . 六边形

查看解析收藏纠错

+选题
6. 丽华根据演讲比赛中九位评委所给的分数作了如下表格
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（　　）

A . 平均数 B . 众数 C . 方差 D . 中位数

查看解析收藏纠错

+选题

7. 在二次函数 $\text{[math]}$ 中，函数y与自变量x的部分对应值如下表：

x	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1	2	3	4	5	6
y	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	2	m	n	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

则m、n的大小关系为 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法比较

查看解析收藏纠错

+选题

8. 两块等腰直角三角形纸片AOB和COD 按图1所示放置，直角顶点重合在点O处，其中AB=3 $\text{[math]}$ ，CD=6.保持纸片AOB不动，将纸片COD绕点O逆时针旋转α（0°<α<90°），如图2所示.当BD与CD在同一直线上（如图3）时，tanα的值等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 我国最大的领海南海总面积有3500 000平方公里，将数3500 000用科学记数法表示应为．

查看解析收藏纠错

+选题
10. 若2x＝3y，且x≠0，则 $\text{[math]}$ 的值为.

查看解析收藏纠错

+选题
11. 若关于x的方程x²﹣8x+m＝0有两个相等的实数根，则m＝．

查看解析收藏纠错

+选题
12. 如图，转盘中6个小扇形的面积相等，任意转动转盘1次，当转盘停止转动时，指针指向红色区域的概率为.

查看解析收藏纠错

+选题
13. 如图，将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上，如果∠1=27°，那么∠2=°

查看解析收藏纠错

+选题
14. 圆锥的底面半径为2，母线长为4，则圆锥的侧面积为（结果保留π）

查看解析收藏纠错

+选题
15. 如图，⊙O的内接四边形ABCD中，∠BOD=100°，则∠BCD=.

查看解析收藏纠错

+选题
16. 计算：4038²－4×2018×2020＝.

查看解析收藏纠错

+选题
17. 如图，菱形OABC中点A的坐标是(2，1)，点B的横坐标是3，则点C的坐标是.

查看解析收藏纠错

+选题
18. 如图，将直线y=x向下平移b个单位长度后得到直线 $\text{[math]}$ ， $\text{[math]}$ 与反比例函数 $\text{[math]}$ （k>0，x＞0）的图象相交于点A，与x轴相交于点B，且 $\text{[math]}$ ，则k的值是.

查看解析收藏纠错

+选题

二、解答题

19.

（1）计算： $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ；

（2）解不等式： $\text{[math]}$ .

查看解析收藏纠错

+选题
20. 先化简再求值： $\text{[math]}$ ，其中 $\text{[math]}$ 是方程 $\text{[math]}$ 的一个根.

查看解析收藏纠错

+选题

21. 为了解某校初二学生每周上网的时间，两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间；小杰从全校400名初二学生中随机抽取了40名学生，调查了每周上网的时间.小丽与小杰整理各自样本数据，如下表所示：

时间段（小时／周）	小丽抽样人数	小杰抽样人数
0～1	6	22
1～2	10	10
2～3	16	6
3～4	8	2

（每组可含最低值，不含最高值）

（1）你认为哪位同学抽取的样本不合理？请说明理由；

（2）根据合理抽取的样本，把上图中的频数分布直方图补画完整；

（3）专家建议每周上网2小时以上（含2小时）的同学应适当减少上网的时间，估计该校全体初二学生中有多少名同学应适当减少上网的时间？

查看解析收藏纠错

+选题

22. 在不透明的袋子中有四张标着数字 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的卡片，这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片，并把卡片上的数字相加.下图是他所画的树状图的一部分.

（1）由上图分析，甲同学的游戏规则是：从袋子中随机抽出一张卡片后（填"放回"或"不放回"），再随机抽出一张卡片；

（2）帮甲同学完成树状图；

（3）求甲同学两次抽到的数字之和为偶数的概率.

查看解析收藏纠错

+选题
23. 如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B.

（1）在图中找出一对相似三角形，并说明理由；

（2）若AB=8，AD= $\text{[math]}$ ，AF= $\text{[math]}$ ，求AE的长.

查看解析收藏纠错

+选题
24. 甲、乙两公司为“见义勇为基金会”各捐款60000元，已知乙公司比甲公司人均多捐40元，甲公司的人数比乙公司的人数多20%．
请你根据以上信息，提出一个用分式方程解决的问题，并写出解答过程．

查看解析收藏纠错

+选题
25. 如图，AB是⊙O的直径， BC交⊙O于点D，E是 $\text{[math]}$ 的中点，连接AE交BC于点F，∠ACB =2∠EAB.

（1）判断直线AC与⊙O的位置关系，并说明理由；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求BF的长.

查看解析收藏纠错

+选题
26. 如图①，老旧电视机屏幕的长宽比为4︰3，但是多数电影图象的长宽比为2.4︰1，故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.

（1）若图①中电视机屏幕为20寸（即屏幕对角线长度）：
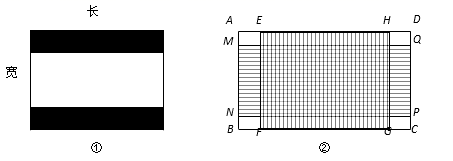
①该屏幕的长＝ ▲ 寸，宽＝ ▲ 寸；

②已知“屏幕浪费比＝黑色带子的总面积：电视机屏幕的总面积”，求该电视机屏幕的浪费比.

（2）为了兼顾电影的收视需求，一种新的屏幕的长宽比诞生了.如图②，这种屏幕（矩形ABCD）恰好包含面积相等且长宽比分别为4︰3的屏幕（矩形EFGH）与2.4︰1的屏幕（矩形MNPQ）.求这种屏幕的长宽比.（参考数据： $\text{[math]}$ ≈2.2，结果精确到0.1）

查看解析收藏纠错

+选题
27. 如图1，对角线互相垂直的四边形叫做垂美四边形.

（1）概念理解：如图2，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；

（2）性质探究：如图1，四边形ABCD的对角线AC、BD交于点O，AC⊥BD.试证明：AB²+CD²＝AD²+BC²；

（3）解决问题：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连结CE、BG、GE.已知AC＝4，AB＝5，求GE的长.

查看解析收藏纠错

+选题
28. 如图，抛物线 $\text{[math]}$ 过点 $\text{[math]}$ ，且与直线 $\text{[math]}$ 交于B、C两点，点B的坐标为 $\text{[math]}$ ．

（1）求抛物线的解析式；

（2）点D为抛物线上位于直线 $\text{[math]}$ 上方的一点，过点D作 $\text{[math]}$ 轴交直线 $\text{[math]}$ 于点E ，点P为对称轴上一动点，当线段 $\text{[math]}$ 的长度最大时，求 $\text{[math]}$ 的最小值；

（3）设点M为抛物线的顶点，在y轴上是否存在点Q ，使 $\text{[math]}$ ？若存在，求点Q的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题

平均数	中位数	众数	方差
8.5	8.3	8.1	0.15

江苏省扬州市广陵区2020年数学中考模拟试卷

一、选择题

二、解答题

相关试卷 收起∨

相关试卷收起∨