江苏省南京市浦口区2020年数学中考二模试卷

修改时间：2024-11-06 浏览次数：278 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 命名为2019-nCoV的新型冠状病毒的大小约125纳米，即0.000000125米.用科学记数法表示0.000000125是（）.

A . 125×10^–7 B . 1.25×10^–7 C . 1.25×10^–6 D . 125×10^–9

查看解析收藏纠错

+选题
2. 计算（－2x²yz）³的结果是（）

A . 8x⁶y³z³ B . －8x⁵y³ z³ C . －6x⁶y³z³ D . －8x⁶y³z³

查看解析收藏纠错

+选题
3. 下列运算中，结果最小的是（）

A . 1－(－2) B . 1－|－2| C . 1×(－2) D . 1÷(－2)

查看解析收藏纠错

+选题
4. 实数a，b，c，d在数轴上的对应点的位置如图所示，则下列结论正确的是（）

A . |a|＞|b| B . a＞﹣3 C . a＞﹣d D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 下列无理数中，与4最接近的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，点A的坐标是(-2，0)，点B的坐标是(0，6)，C为OB的中点，将△ABC绕点B逆时针旋转90°后得到 $\text{[math]}$ ．若反比例函数 $\text{[math]}$ 的图象恰好经过 $\text{[math]}$ 的中点D，则k的值是（）

A . 9 B . 12 C . 15 D . 18

查看解析收藏纠错

+选题

二、填空题

7. － $\text{[math]}$ 的相反数是； $\text{[math]}$ 的倒数是.

查看解析收藏纠错

+选题
8. 计算 $\text{[math]}$ － $\text{[math]}$ 的结果是.

查看解析收藏纠错

+选题
9. 分解因式：4a²-64=.

查看解析收藏纠错

+选题
10. 若方程 $\text{[math]}$ 的两根 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

查看解析收藏纠错

+选题
11. 将一个矩形纸片折叠成如图所示的图形，若∠ABC=26°，则∠ACD=.

查看解析收藏纠错

+选题
12. 如图，已知点E在正方形ABCD的边AB上，以BE为边向正方形ABCD外部作正方形BEFG，连接DF，M、N分别是DC、DF的中点，连接MN，若AB＝9，BE＝6，则MN的长为.

查看解析收藏纠错

+选题

13. 为了解某区初中学生对网络游戏的喜好和作业量多少情况，随机抽取了该区500名同学进行了调查，并将调查的情况进行了整理，如下表：

作业量多少

网络游戏的喜好

认为作业多

认为作业不多

合计

喜欢网络游戏

180

270

不喜欢网络游戏

150

230

根据抽样调查结果，估计该区12000名初中生“不喜欢网络游戏并认为作业不多”的人数是.

查看解析收藏纠错

+选题

14. 如图，五边形 ABCDE 是⊙O 的内接正五边形， AF 是⊙O 的直径，则∠ BDF 的度数是°

查看解析收藏纠错

+选题
15. “低碳生活，绿色出行”是一种环保、健康的生活方式，小丽从甲地出发沿一条笔直的公路骑行前往乙地，她与乙地之间的距离y(km)与出发时间t（h）之间的函数关系如图中线段AB所示，在小丽出发的同时，小明从乙地沿同一条公路汽骑车匀速前往甲地，两人之间的距离s(km)与出发时间t（h）之间的函数关系如图中折线段AD－DE－EF所示，则E点坐标为
.

查看解析收藏纠错

+选题
16. 如图，在△ABC中，∠ACB=90°，BC=12，AC=9，以点C为圆心，6为半径的圆上有一个动点D.连接AD、BD、CD，则2AD+3BD的最小值是.

查看解析收藏纠错

+选题

三、解答题

17. 计算（2a－b＋1）(2a－1－b)

查看解析收藏纠错

+选题
18. 解不等式组 $\text{[math]}$ ，并写出它的所有非负整数解.

查看解析收藏纠错

+选题

19. 丁老师为了解所任教的两个班的学生数学学习情况，对数学进行了一次测试，获得了两个班的成绩（百分制），并对数据（成绩）进行整理、描述和分析，下面给出了部分信息.

①A、B两班学生（两个班的人数相同）数学成绩不完整的频数分布直方图如下（数据分成5组：x<60，60≤x<70，70≤x<80，80≤x<90，90≤x≤100）：

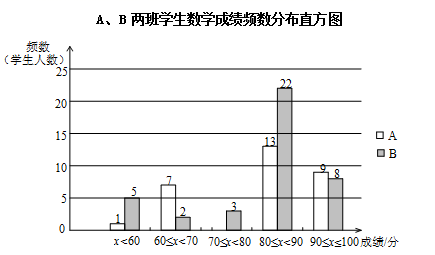
②A、B两班学生测试成绩在80≤x<90这一组的数据如下：

A班：80 80 82 83 85 85 86 87 87 87 88 89 89

B班：80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89

③A、B两班学生测试成绩的平均数、中位数、方差如下：

	平均数	中位数	方差
A班	80.6	m	96.9
B班	80.8	n	153.3

根据以上信息，回答下列问题：

（1）补全数学成绩频数分布直方图；

（2）写出表中m、n的值；

（3）请你对比分析A、B两班学生的数学学习情况（至少从两个不同的角度分析）.

查看解析收藏纠错

+选题

20. 一个不透明的布袋中仅有2个红球、1个黑球，这些球除颜色外无其他差别.

（1）甲同学先随机摸出一个小球，记下颜色后放回搅匀，再随机摸出一个小球，则两次摸出的小球颜色不同的概率是多少？

（2）乙同学从中一次摸出两个球，则摸出的小球均为红色的概率是.

查看解析收藏纠错

+选题
21. 货车行驶25千米与汽车行驶35千米所用时间相同，已知汽车每小时比货车多行驶20千米，求两车的速度各为多少?

查看解析收藏纠错

+选题
22. 如图，在菱形ABCD中，对角线AC、BD交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF＝BE，连接DF.

（1）求证：四边形AEFD是矩形；

（2）若BF＝8，DF＝4，求CD的长.

查看解析收藏纠错

+选题
23. 数学兴趣小组到黄河风景名胜区测量炎帝塑像（塑像中高者）的高度.如图所示，炎帝塑像DE在高55 m的小山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进21 m到达B处，测得塑像顶部D的仰角为60°，求炎帝塑像DE的高度.（精确到1 m.参考数据：tan34°≈0.67，tan60°= $\text{[math]}$ 1.73）

查看解析收藏纠错

+选题
24. 如图，点 $\text{[math]}$ 在半径为8的 $\text{[math]}$ 上，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ．连接 $\text{[math]}$ ，且 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；

（2）求图中阴影部分的面积．

查看解析收藏纠错

+选题
25. 随着 $\text{[math]}$ 技术的发展，人们对各类 $\text{[math]}$ 产品的使用充满期待.某公司计划在某地区销售第一款 $\text{[math]}$ 产品，根据市场分析，该产品的销售价格将随销售周期的变化而变化.设该产品在第 $\text{[math]}$ （ $\text{[math]}$ 为正整数）个销售周期每台的销售价格为 $\text{[math]}$ 元， $\text{[math]}$ 与 $\text{[math]}$ 之间满足如图所示的一次函数关系.

（1）求 $\text{[math]}$ 与 $\text{[math]}$ 之间的关系式；

（2）设该产品在第 $\text{[math]}$ 个销售周期的销售数量为 $\text{[math]}$ （万台）， $\text{[math]}$ 与 $\text{[math]}$ 的关系可用 $\text{[math]}$ 来描述。根据以上信息，试问：哪个销售周期的销售收入最大？此时该产品每台的销售价格是多少元？

查看解析收藏纠错

+选题
26. 在平面直角坐标系xOy中，已知抛物线y＝x²﹣mx+n.

（1）当m＝2时，
①求抛物线的对称轴，并用含n的式子表示顶点的纵坐标；

②若点A（﹣2，y₁），B（x₂ ， y₂）都在抛物线上，且y₂＞y₁ ，求x₂的取值范围；

（2）已知点P（﹣1，2），将点P向右平移4个单位长度，得到点Q.当n＝3时，若抛物线与线段PQ恰有一个公共点，结合函数图象，求m的取值范围.

查看解析收藏纠错

+选题
27. 如图1，在矩形ABCD中，BC=3，动点P从B出发，以每秒1个单位的速度，沿射线BC方向移动，作△PAB关于直线PA的对称△PAB' ，设点P的运动时间为t（s）.

（1）若AB=2 $\text{[math]}$ .
①如图2，当点B' 落在AC上时，求t的值；

②是否存在异于图2的时刻，使得△PCB’是直角三角形？若存在，请直接写出所有符合题意的t值？若不存在，请说明理由.

（2）若四边形ABCD是正方形，直线PB'与直线CD相交于点M，当点P不与点C重合时，求证：∠PAM=45°.

查看解析收藏纠错

+选题

江苏省南京市浦口区2020年数学中考二模试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨