修改时间:2024-11-06 浏览次数:291 类型:中考模拟
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
|
分数 人数 班级 |
60 |
70 |
80 |
90 |
100 |
|
1班 |
0 |
1 |
6 |
2 |
1 |
|
2班 |
1 |
1 |
3 |
a |
1 |
|
3班 |
1 |
1 |
4 |
2 |
2 |
分析数据:
|
平均数 |
中位数 |
众数 |
|
|
1班 |
83 |
80 |
80 |
|
2班 |
83 |
c |
d |
|
3班 |
b |
80 |
80 |
根据以上信息回答下列问题:
|
x |
… |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
|
y |
… |
3 |
m |
1 |
0 |
1 |
2 |
1 |
n |
|
… |
其中,m= , n=.
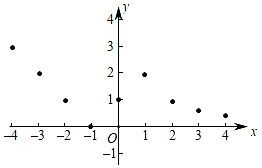
①点A( ,y1),B(5,y2),C(x1 ,
),D(x2 , 6)在函数图象上,则y1 ▲ y2 , x1 ▲ x2;(填“>”,“=”或“<”)
②当函数值y=1时,求自变量x的值;
试题篮