初中数学中考复习综合专题：二次函数应用题

修改时间：2020-06-24 浏览次数：531 类型：一轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、综合题

1. 某超市销售一种文具，进价为 5（元/件），售价为6（元/件）时，当天的销售量为100件，在销售过程中发现：售价每上涨0.5元，当天的销售量就减少5件，设当天销售单价统一为 $\text{[math]}$ （元/件）（ $\text{[math]}$ ，且 $\text{[math]}$ 是按0.5元的倍数上涨），当天销售利润为 $\text{[math]}$ 元.

（1）求 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式（不要求写出自变量的取值范围）；

（2）要使当天销售利润不低于240元，求当天销售单价的范围；

（3）若每件文具的利润不超过60%，要使当天获得利润最大，每件文具售价为多少元？并求出最大利润.

查看解析收藏纠错

+选题

2. 受“新冠”疫情的影响，某销售商在网上销售 $\text{[math]}$ 、 $\text{[math]}$ 两种型号的“手写板”，获利颇丰.已知 $\text{[math]}$ 型， $\text{[math]}$ 型手写板进价、售价和每日销量如表格所示：

	进价（元/个）	售价（元/个）	销量（个/日）
$\text{[math]}$ 型	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$ 型	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

根据市场行情，该销售商对 $\text{[math]}$ 型手写板降价销售，同时对 $\text{[math]}$ 型手写板提高售价，此时发现 $\text{[math]}$ 型手写板每降低 $\text{[math]}$ 元就可多卖 $\text{[math]}$ 个， $\text{[math]}$ 型手写板每提高 $\text{[math]}$ 元就少卖 $\text{[math]}$ 个，要保持每天销售总量不变，设其中 $\text{[math]}$ 型手写板每天多销售 $\text{[math]}$ 个，每天总获利的利润为 $\text{[math]}$ 元

（1）求y与x之间的函数关系式并写出x的取值范围；

（2）要使每天的利润不低于 $\text{[math]}$ 元，直接写出x的取值范围；

（3）该销售商决定每销售一个B型手写板，就捐a元给(0< a≤100)因“新冠疫情”影

响的困难家庭，当30≤x≤40时，每天的最大利润为229200元，求a的值.

查看解析收藏纠错

+选题

3. 某商场出售一款速干毛巾，其成本为20元/条，销售中发现，该商品每天的销售量y（条）与销售单价x（元/条）之间存在如图所示的关系。

（1）请求出y与x的函数关系式；

（2）该款速干毛巾销售单价定为多少元时，每天销售利润最大？最大利润是多少元？

（3）近期武汉爆发了“新型冠状病毒”疫情，该商场店主决定从每天获得的利润中抽出200元捐赠给武汉，为了保证捐款后每天剩余利润不低于550元，如何确定该款速干毛巾的销售单价？

查看解析收藏纠错

+选题
4. 海鲜门市的某种海鲜食材，成本为10元/千克，每天的进货量p（千克）与销售价格x（元/千克）满足函数关系式 $\text{[math]}$ ，从市场反馈的信息发现，该海鲜食材每天的市场需求量q（千克）与销售价格x（元/千克）满足一次函数关系，部分数据如下表：

销售价格x（元/千克）

10

12

…

30

市场需求量q（千克）

30

28

…

10

（已知按物价部门规定销售价格x不低于10元/千克且不高于30元/千克）

（1）请写出q与x的函数关系式：；

（2）当每天的进货量小于或等于市场需求量时，这种海鲜食材能全部售出，而当每天的进货量大于市场需求量时，只能售出符合市场需求量的海鲜食材，剩余的海鲜食材由于保质期短而只能废弃.
①求出每天获得的利润y（元）与销售价格x的函数关系式；

②为了避免浪费，每天要确保这种海鲜食材能全部售出，求销售价格为多少元时，每天获得的利润（元）最大值是多少？

查看解析收藏纠错

+选题
5. 商场某种商品平均每天可销售40件，每件盈利60元．为减少库存，商场决定采取适当的降价措施．经调查发现，每件商品每降价1元，商场平均每天可多销售2件．

（1）每件商品降价多少元时，商场日盈利可达到3150元？

（2）商场日盈利能否达到3300元？

（3）每件商品降价多少元时，商场日盈利最多？

查看解析收藏纠错

+选题
6. 某种蔬菜每千克售价y₁（元）与销售月份x之间的关系如图1所示，每千克成本y₂（元）与销售月份x之间的关系如图2所示，其中图1中的点在同一条线段上，图2中的点在对称轴平行于y轴的同一条抛物线上，且抛物线的最低点的坐标为（6，1）.

（1）求出y₁与x函数关系式；

（2）求出y₂与x函数关系式；

（3）设这种蔬菜每千克收益为w元，试问在哪个月份出售这种蔬菜，w将取得最大值？并求出此最大值.（收益＝售价﹣成本）

查看解析收藏纠错

+选题
7. 红灯笼，象征着阖家团圆，红红火火，挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼，用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同，已知乙灯笼每对进价比甲灯笼每对进价多9元.

（1）求甲、乙两种灯笼每对的进价；

（2）经市场调查发现，乙灯笼每对售价50元时，每天可售出98对，售价每提高1元，则每天少售出2对：物价部门规定其销售单价不高于每对65元，设乙灯笼每对涨价x元，小明一天通过乙灯笼获得利润y元.
①求出y与x之间的函数解析式；

②乙种灯笼的销售单价为多少元时，一天获得利润最大？最大利润是多少元？

查看解析收藏纠错

+选题
8. 大学生小李和同学一起自主创业开办了一家公司，公司对经营的盈亏情况在每月的最后一天结算一次.在1－12月份中，该公司前x个月累计获得的总利润y（万元）与销售时间x（月）之间满足二次函数关系.

（1）求y与x函数关系式.

（2）该公司从哪个月开始“扭亏为盈”（当月盈利）? 直接写出9月份一个月内所获得的利润.

（3）在前12 个月中，哪个月该公司所获得利润最大？最大利润为多少？

查看解析收藏纠错

+选题
9. 我市某童装专卖店在销售中发现，一款童装每件进价为40元，若销售价为60元，每天可售出20件，为迎接“双十一”，专卖店决定采取适当的降价措施，以扩大销售量，经市场调查发现，如果每件童装降价1元，那么平均可多售出2件 $\text{[math]}$ 设每件童装降价x元 $\text{[math]}$ 时，平均每天可盈利y元．

（1）写出y与x的函数关系式；

（2）当该专卖店每件童装降价多少元时，平均每天盈利400元？

（3）该专卖店要想平均每天盈利600元，可能吗？请说明理由．

查看解析收藏纠错

+选题
10. 唐山世园会期间，游乐场投资150万元引进一项大型游乐设施．若不计维修保养费用，预计开放后每月可创收31万元．而该游乐场开放后，从第1个月到第x个月的维修保养费用累计为y（万元），且y＝ax²＋bx．若将创收扣除投资和维修保养费用称为游乐场的纯收益g（万元），g也是关于x的二次函数．

（1）若维修保养费用第1个月为2万元，第2个月为4万元，求y关于x的解析式；

（2）求纯收益g关于x的解析式；

（3）问设施开放几个月后，游乐场的纯收益达到最大？并求出最大收益．

查看解析收藏纠错

+选题
11. 每年十月的第二个周四是世界爱眼日，为预防近视，超市决定对某型号护眼台灯进行降价销售．降价前，进价为30元的护眼台灯以80元售出，平均每月能售出200盏，调查表明：这种护眼台灯每盏售价每降低1元，其月平均销售量将增加10盏．

（1）写出月销售利润y（单位：元）与销售价x（单位：元/盏）之间的函数表达式；

（2）当销售价定为多少元时，所得月利润最大？最大月利润为多少元？

查看解析收藏纠错

+选题
12. 华联超市准备代销一款运动鞋，每双的成本是170元，为了合理定价，投放市场进行试销.据市场调查，销售单价是200元时，每天的销售量是40双，而销售单价每降低1元，每天就可多售出5双，设每双降低x元(x为正整数)，每天的销售利润为y元.

（1）求y与x的函数关系式；

（2）每双运动鞋的售价定为多少元时，每天可获得最大利润？最大利润是多少？

查看解析收藏纠错

+选题
13. 随着城市化建设的发展，交通拥堵成为上班高峰时难以避免的现象．为了解龙泉驿某条道路交通拥堵情况，龙泉某中学同学经实地统计分析研究表明：当 $\text{[math]}$ 时，车流速度v（千米/小时）是车流密度x（辆/千米）的一次函数．当该道路的车流密度达到220辆/千米时，造成堵塞，此时车流速度为0千米/小时；当车流密度为95辆/千米时，车流速度为50千米/小时．

（1）当 $\text{[math]}$ 时，求车流速度v（千米/小时）与车流密度x（辆/千米）的函数关系式；

（2）为使该道路上车流速度大于40千米/小时且小于60千米/小时，应控制该道路上的车流密度在什么范围内？

（3）车流量（辆/小时）是单位时间内通过该道路上某观测点的车辆数，即：车流量=车流速度×车流密度．当 $\text{[math]}$ 时，求该道路上车流量y的最大值．此时车流速度为多少？

查看解析收藏纠错

+选题
14. 草莓是云南多地盛产的一种水果，今年某水果销售店在草莓销售旺季试销售成本为每千克18元的草莓，规定试销期间销售单价不低于成本单价，也不高于每千克40元．经试销发现，销售量y（kg）与销售单价x（元/kg）符合一次函数关系，如图是y与x的函数关系图象．

（1）求y与x的函数解析式；

（2）设该水果销售店试销草莓获得的利润为W元，求W的最大值．

查看解析收藏纠错

+选题
15. 某批发部某一玩具价格如图所示，现有甲、乙两个商店，计划在“六一”儿童节前到该批发部购买此类玩具，两商店所需玩具总数为120个，乙商店所需数量不超过50个，设甲商店购买 $\text{[math]}$ 个，如果甲、乙两商店分别购买玩具，两商店需付款总和为 $\text{[math]}$ 元.

（1）求y关于x的函数关系式，并写出自变量x的取值范围；

（2）若甲商店购买不超过100个，请说明甲、乙两商店联合购买比分别购买最多可节约多少钱？

查看解析收藏纠错

+选题
16. “创科集团”会议室内的一个长为6米、宽为4米的矩形ABCD墙面需要进行装饰，设计图案如图所示，将矩形ABCD墙面分割成3个区域，中间“十”字形区域甲的宽度均为1米，四个角为四个全等的直角三角形，△AEF，△BGH，△CMN，△DPQ为区域乙，剩下部分为区域丙，其中AE=BG=CN=DP，设EG=HM=NP=FQ=x(米)(1≤x≤3)

（1）当x=2时，求区域乙的面积；

（2）求区域丙的面积的最大值；

（3）为了图案富有美感，设置区域乙与区域丙的面积之比为1：4，在区域甲、区域乙、区域丙分别嵌贴甲、乙、丙三种不同的装饰板，这三种装饰板每平方米的单价分别为a(百元)，b(百元)，c(百元)(a，b，c均为整数，且6<a<10)，若a+b+c=20，整个墙面嵌贴共花费了150(百元)，求三种装饰板每平方米的单价。

查看解析收藏纠错

+选题
17. 衢州某科技生态农业养殖有限公司种植和销售一种绿色羊肚菌，已知该羊肚菌的成本是12元/千克，规定销售价格不得低于成本，且不能高于成本的两倍。经过市场调查发现，某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)之间的函数关系如下图所示。

（1）求y与x之间的函数解析式。

（2）求这一天销售羊肚菌获得的利润W的最大值。

（3）若该公司按每销售一千克提取1元用于捐资助学，且保证每天的销售利润不低于3600元，则该羊肚菌销售价格该如何确定？

查看解析收藏纠错

+选题
18. 为满足市场需求，新生活超市在端午节前夕购进价格为3元/个的粽子，根据市场预测，该品牌粽子每个售价4元时，每天能出售500个，并且售价每上涨0.1元，其销售量将减少10个，为了维护消费者利益，物价部门规定，该品牌粽子的售价不能超过进价的200%。

（1）请你利用所学知识帮助超市给该品牌粽子定价，使超市每天的销售利润为800元。

（2）定价为多少时每天的利润最大？最大利润是多少？

查看解析收藏纠错

+选题
19. 随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进，拥有的养老床位及养老建筑不断增加。

（1）该市的养老床位数从2017年底的2万个增长到2019年底的2.88万个，求该市这两年(从2017年底到2019年底)拥有的养老床位数的平均年增长率；

（2）该市某社区今年准备新建一养老中心，如果计划赡养200名老人，建筑投入平均5万元/人，且计划赡养的老人每增加5人，建筑投入平均减少1000元/人，那么新建该养老中心需申报的最高建筑投入是多少？

查看解析收藏纠错

+选题
20. 为鼓励大学毕业生自主创业，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件元，出厂价为每件元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数： $\text{[math]}$ .

（1）李明在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元?

（2）设李明获得的利润为W（元），当销售单价定为多少元时，每月可获得最大利润?

（3）物价部门规定，这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元?

查看解析收藏纠错

+选题
21. 某品牌服装公司经过市场调査，得到某种运动服的月销量 y(件)是售价 x(元/件)的一次函数，其售价、月销售量、月销售利润 w(元)的三组对应值如下表：

注：月销售利润＝月销售量×(售价一进价)

（1）求 y 关于 x 的函数解析式(不要求写出自变量的取值范围)；

（2）当售价是多少时，月销售利润最大？最大利润是多少元？

（3）为响应号召，该公司决定每售出 1 件服装，就捐赠 a 元(a > 0)，商家规定该服装售价不得超过200 元，月销售量仍满足上关系，若此时月销售最大利润仍可达 9600 元，求 a 的值.

查看解析收藏纠错

+选题
22. 某药厂销售部门根据市场调研结果，对该厂生产的一种新型原料药未来两年的销售进行预测，并建立如下模型：设第t个月该原料药的月销售量为P（单位：吨），P与t之间存在如图所示的函数关系，其图象是函数P= $\text{[math]}$ （0＜t≤8）的图象与线段AB的组合；设第t个月销售该原料药每吨的毛利润为Q（单位：万元），Q与t之间满足如下关系：Q= $\text{[math]}$

（1）当8＜t≤24时，求P关于t的函数解析式；

（2）设第t个月销售该原料药的月毛利润为w（单位：万元）
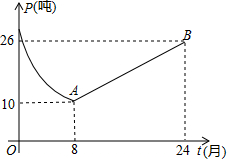
①求w关于t的函数解析式；

②该药厂销售部门分析认为，336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围，求此范围所对应的月销售量P的最小值和最大值．

查看解析收藏纠错

+选题
23. 小明大学毕业回家乡创业，第一期培植盆景与花卉各40盆售后统计，盆景的平均每盆利润是160元，花卉的平均每盆利润是19元，调研发现：
①盆景每增加1盆，盆景的平均每盆利润减少2元；每减少1盆，盆景的平均每盆利润增加2元；②花卉的平均每盆利润始终不变．

小明计划第二期培植盆景与花卉共80盆，设培植的盆景比第一期增加x盆，第二期盆景与花卉售完后的利润分别为W₁ ， W₂（单位：元）

（1）用含x的代数式分别表示W₁ ， W₂；

（2）当x取何值时，第二期培植的盆景与花卉售完后获得的总利润W最大，最大总利润是多少？

查看解析收藏纠错

+选题

24. 某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为8.1元/斤，并且两次降价的百分率相同．

（1）求该种水果每次降价的百分率；

（2）从第一次降价的第1天算起，第x天（x为整数）的售价、销量及储存和损耗费用的相关信息如表所示．已知该种水果的进价为4.1元/斤．

时间x（天）	1≤x＜9	9≤x＜15
售价（元/斤）	第1次降价后的价格	第2次降价后的价格
销量（斤）	80﹣3x	120﹣x
储存和损耗费用（元）	40+3x	3x²﹣64x+400

设销售该水果第x（天）的利润为y（元），求y与x（1≤x＜15）之间的函数解析式，并求出第几天时销售利润最大．

查看解析收藏纠错

+选题

25. 某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利50元，为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件.求：

（1）若商场平均每天要赢利1600元，每件衬衫应降价多少元？

（2）每件衬衫降价多少元时，商场平均每天赢利最多？

查看解析收藏纠错

+选题
26. 某超市拟于中秋节前 $\text{[math]}$ 天里销售某品牌月饼，其进价为 $\text{[math]}$ 元/ $\text{[math]}$ .设第 $\text{[math]}$ 天的销售价格为 $\text{[math]}$ （元/ $\text{[math]}$ ），销售量为 $\text{[math]}$ .该超市根据以往的销售经验得出以下的销售规律：①当 $\text{[math]}$ 时， $\text{[math]}$ ；当 $\text{[math]}$ 时， $\text{[math]}$ 与 $\text{[math]}$ 满足一次函数关系，且当 $\text{[math]}$ 时， $\text{[math]}$ ； $\text{[math]}$ 时， $\text{[math]}$ .② $\text{[math]}$ 与 $\text{[math]}$ 的关系为 $\text{[math]}$ .

（1）当 $\text{[math]}$ 时， $\text{[math]}$ 与 $\text{[math]}$ 的关系式为；

（2） $\text{[math]}$ 为多少时，当天的销售利润 $\text{[math]}$ （元）最大？最大利润为多少？

（3）若超市希望第 $\text{[math]}$ 天到第 $\text{[math]}$ 天的日销售利润 $\text{[math]}$ （元）随 $\text{[math]}$ 的增大而增大，则需要在当天销售价格的基础上涨 $\text{[math]}$ 元/ $\text{[math]}$ ，求 $\text{[math]}$ 的最小值.

查看解析收藏纠错

+选题
27. 小王电子产品专柜以20元/副的价格批发了某新款耳机，在试销的60天内整理出了销售数据如下

销售数据(第x天)

售价(元)

日销售量(副)

1≤x＜35

x+30

100﹣2x

35≤x≤60

70

100﹣2x

（1）若试销阶段每天的利润为W元，求出W与x的函数关系式；

（2）请问在试销阶段的哪一天销售利润W可以达到最大值？最大值为多少？

查看解析收藏纠错

+选题
28. 某商场用两个月时间试销某种新型商品，经市场调查，该商品的第 $\text{[math]}$ 天的进价 $\text{[math]}$ （元／件）与 $\text{[math]}$ （天）之间的相关信息如下表：

时间 $\text{[math]}$ （天）

$\text{[math]}$

$\text{[math]}$

进价 $\text{[math]}$ （元／件）

$\text{[math]}$

40

该商品在销售过程中，销售量 $\text{[math]}$ （件）与 $\text{[math]}$ （天）之间的函数关系如图所示：

在销售过程中，商场每天销售的该产品以每件80元的价格全部售出.

（1）求该商品的销售量 $\text{[math]}$ （件）与 $\text{[math]}$ （天）之间的函数关系；

（2）设第 $\text{[math]}$ 天该商场销售该商品获得的利润为 $\text{[math]}$ 元，求出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式，并求出第几天销售利润最大，最大利润是多少元？

（3）在销售过程中，当天的销售利润不低于2400元的共有多少天？

查看解析收藏纠错

+选题
29. 每年5月的第二个星期日即为母亲节，“父母恩深重，恩怜无歇时”，许多市民喜欢在母亲节为母亲送花，感恩母亲，祝福母亲…今年节日前夕，某花店采购了一批康乃馨，经分析上一年的销售情况，发现这种康乃馨每天的销售量y（支）是销售单价x（元）的一次函数，已知销售单价为7元/支时，销售量为16支；销售单价为8元/支时，销售量为14支。

（1）求这种康乃馨每天的销售量y（支）关于销售单价x（元/支）的一次函数解析式；

（2）若按去年方式销售，已知今年这种康乃馨的进价是每支5元，商家若想每天获得42元的利润，销售单价要定为多少元？

（3）在（2）的条件下，当销售单价x为何值时，花店销售这种康乃馨每天获得的利润最大？并求出获得的最大利润。

查看解析收藏纠错

+选题
30. 某手机专营店，第一期进了甲种手机50部．售后统计，甲种手机的平均利润是160元/部．调研发现：甲种手机每增加1部，平均利润减少2元/部；该店计划第二期进货甲种手机比第一期增加x部，

（1）第二期甲种手机售完后的利润为8400元，那么甲种手机比第一期要增加多少部?

（2）当x取何值时，第二期进的甲种手机售完后获得的利润W最大，最大利润是多少？

查看解析收藏纠错

+选题

销售价格x（元/千克）	10	12	…	30
市场需求量q（千克）	30	28	…	10

销售数据(第x天)	售价(元)	日销售量(副)
1≤x＜35	x+30	100﹣2x
35≤x≤60	70	100﹣2x

时间 $\text{[math]}$ （天）	$\text{[math]}$	$\text{[math]}$
进价 $\text{[math]}$ （元／件）	$\text{[math]}$	40

初中数学中考复习综合专题：二次函数应用题

一、综合题

相关试卷 收起∨

相关试卷收起∨