上海市协和双语学校2020年中考数学一模考试试卷

修改时间：2024-07-31 浏览次数：264 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 函数y=﹣2x²先向右平移1个单位，再向下平移2个单位，所得函数解析式是（）

A . y=﹣2（x﹣1）²+2 B . y=﹣2（x﹣1）²﹣2 C . y=﹣2（x+1）²+2 D . y=﹣2（x+1）²﹣2

查看解析收藏纠错

+选题
2. 在Rt△ABC中，∠C＝90°，若BC＝3，AC＝4，则sinB的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 下列说法中，正确是（）

A . 如果k＝0， $\text{[math]}$ 是非零向量，那么k $\text{[math]}$ ＝0 B . 如果 $\text{[math]}$ 是单位向量，那么 $\text{[math]}$ ＝1 C . 如果| $\text{[math]}$ |＝| $\text{[math]}$ |，那么 $\text{[math]}$ ＝ $\text{[math]}$ 或 $\text{[math]}$ ＝﹣ $\text{[math]}$ D . 已知非零向量 $\text{[math]}$ ，如果向量 $\text{[math]}$ ＝﹣5 $\text{[math]}$ ，那么 $\text{[math]}$ ∥ $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图，在6×6的正方形网格中，联结小正方形中两个顶点A、B ，如果线段AB与网格线的其中两个交点为M、N ，那么AM：MN：NB的值是（）

A . 3：5：4 B . 3：6：5 C . 1：3：2 D . 1：4：2

查看解析收藏纠错

+选题
5. 使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m³）与旋钮的旋转角度x（单位：度）（0°＜x≤90°）近似满足函数关系y＝ax²+bx+c（a≠0）．如图记录了某种家用节能燃气灶烧开同一壶水的旋钮的旋转角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮的旋转角度约为（）

A . 33° B . 36° C . 42° D . 49°

查看解析收藏纠错

+选题
6. 如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F ，连结BD、DP ， BD与CF相交于点H ，给出下列结论：①BE＝2AE；②△DFP∽△BPH；③DP²＝PH•PC；④FE：BC＝ $\text{[math]}$ ，其中正确个数为（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题

二、填空题

7. 如果 $\text{[math]}$ ，那么锐角 $\text{[math]}$ 的度数是.

查看解析收藏纠错

+选题
8. 已知 $\text{[math]}$ ，那么 $\text{[math]}$ =．

查看解析收藏纠错

+选题
9. 已知线段AB=2，P是AB的黄金分割点，且AP > BP ，那么AP=．

查看解析收藏纠错

+选题
10. 已知点A（x₁ ， y₁）、B（x₂ ， y₂）为抛物线y＝（x﹣2）²上的两点，如果x₁＜x₂＜2，那么y₁y₂ ．（填“＞”“＜”或“＝”）

查看解析收藏纠错

+选题
11. 如果点A(﹣3，y₁)和点B(﹣2，y₂)是抛物线y＝x²+a上的两点，那么y₁y₂ ．（填“＞”、“＝”、“＜”）．

查看解析收藏纠错

+选题
12. 抛物线 $\text{[math]}$ 在对称轴右侧的部分是的.(填“上升”或“下降”)

查看解析收藏纠错

+选题
13. 如图，某小区门口的栏杆从水平位置AB绕固定点O旋转到位置DC ，已知栏杆AB的长为3.5米，OA的长为3米，点C到AB的距离为0.3米，支柱OE的高为0.6米，那么栏杆端点D离地面的距离为米

查看解析收藏纠错

+选题
14. 如图，在菱形ABCD中，O、E分别是AC、AD的中点，联结OE ．如果AB=3，AC=4，那么cot∠AOE=．

查看解析收藏纠错

+选题
15. 如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝3， BC＝2，tanA＝ $\text{[math]}$ ，则CD＝．

查看解析收藏纠错

+选题
16. 已知在Rt△ABC中，∠C=90º，AC=3，BC=4，⊙C与斜边AB相切，那么⊙C的半径为.

查看解析收藏纠错

+选题
17. 在方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．如图，请在边长为1个单位的2×3的方格纸中，找出一个格点三角形DEF ．如果△DEF与△ABC相似（相似比不为1），那么△DEF的面积为．

查看解析收藏纠错

+选题
18. 如图，在等腰△ABC中，AB=AC=4，BC=6点D在底边BC上，且∠DAC=∠ACD，将△ACD沿着AD所在直线翻折，使得点C落到点E处，联结BE，那么BE的长为.

查看解析收藏纠错

+选题

三、解答题

19. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
20. 已知：在平行四边形ABCD中，AB︰BC=3︰2.

（1）根据条件画图：作∠BCD的平分线，交边AB于点E，取线段BE的中点F，连接DF交CE于点G.

（2）设 $\text{[math]}$ ，那么向量 $\text{[math]}$ =.(用向量 $\text{[math]}$ 、 $\text{[math]}$ 表示)，并在图中画出向量 $\text{[math]}$ 在向量 $\text{[math]}$ 和 $\text{[math]}$ 方向上的分向量.

查看解析收藏纠错

+选题
21. 如图1为放置在水平桌面l上的台灯，底座的高AB为5cm ，长度均为20cm的连杆BC、CD与AB始终在同一平面上．

（1）转动连杆BC ， CD ，使∠BCD成平角，∠ABC＝150°，如图2，求连杆端点D离桌面l的高度DE ．

（2）将（1）中的连杆CD再绕点C逆时针旋转，经试验后发现，如图3，当∠BCD＝150°时台灯光线最佳．求此时连杆端点D离桌面l的高度比原来降低了多少厘米？

查看解析收藏纠错

+选题
22. 如图，梯形ABCD中，AD∥BC，∠ADC=90º，AD= 2，BC= 4， $\text{[math]}$ .以AB为直径作⊙O，交边DC于E、F两点.

（1）求证：DE=CF.

（2）求直径AB的长.

查看解析收藏纠错

+选题
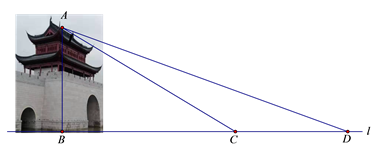
23. 水城门位于淀浦河和漕港河三叉口，是环城水系公园淀浦河梦蝶岛区域重要的标志性景观．在课外实践活动中，某校九年级数学兴趣小组决定测量该水城门的高．他们的操作方法如下：如图，先在D处测得点A的仰角为20°，再往水城门的方向前进13米至C处，测得点A的仰角为31°（点D、C、B在一直线上），求该水城门AB的高．（精确到0.1米）
（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）

查看解析收藏纠错

+选题
24. 已知：在平面直角坐标系xOy中，对称轴为直线x = -2的抛物线经过点C(0，2)，与x轴交于A(-3，0)、B两点(点A在点B的左侧).

（1）求这条抛物线的表达式.

（2）连接BC，求∠BCO的余切值.

（3）如果过点C的直线，交x轴于点E，交抛物线于点P，且∠CEO =∠BCO，求点P的坐标.

查看解析收藏纠错

+选题
25. 如图，在△ABC中，AB＝AC＝10，BC＝16，点D为BC边上的一个动点（点D不与点B、点C重合）．以D为顶点作∠ADE＝∠B ，射线DE交AC边于点E ，过点A作AF⊥AD交射线DE于点F ．

（1）求证：AB•CE＝BD•CD；

（2）当DF平分∠ADC时，求AE的长；

（3）当△AEF是等腰三角形时，求BD的长．

查看解析收藏纠错

+选题

上海市协和双语学校2020年中考数学一模考试试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨