2017年浙江中考真题分类汇编（数学）：专题15 压轴题

1.
在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC，连结OB，D为OB的中点。点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF。已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒。

（1）如图1，当t=3时，求DF的长；

（2）如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值；

（3）连结AD，当AD将△DEF分成的两部分面积之比为1：2时，求相应t的值。

查看解析收藏纠错

+选题
2.
如图，在矩形ABCD中，点E是AD上的一个动点，连接BE，作点A关于BE的对称点F，且点F落在矩形ABCD的内部，连结AF，BF，EF，过点F作GF⊥AF交AD于点G，设 $\text{[math]}$ =n.

（1）求证：AE=GE；

（2）当点F落在AC上时，用含n的代数式表示 $\text{[math]}$ 的值；

（3）若AD=4AB，且以点F，C，G为顶点的三角形是直角三角形，求n的值.

查看解析收藏纠错

+选题

3.
如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，

（1）点点同学通过画图和测量得到以下近似数据：
ɑ
30°
40°
50°
60°
β
120°
130°
140°
150°
γ
150°
140°
130°
120°
猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：

（2）若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．

查看解析收藏纠错

+选题
4.
如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．

（1）当∠APB=28°时，求∠B和 $\text{[math]}$ 的度数；

（2）求证：AC=AB．

（3）在点P的运动过程中
①当MP=4时，取四边形ACDE一边的两端点和线段MP上一点Q，若以这三点为顶点的三角形是直角三角形，且Q为锐角顶点，求所有满足条件的MQ的值；
②记AP与圆的另一个交点为F，将点F绕点D旋转90°得到点G，当点G恰好落在MN上时，连结AG，CG，DG，EG，直接写出△ACG和△DEG的面积之比．

查看解析收藏纠错

+选题
5. 有两个内角分别是它们对角的一半的四边形叫做半对角四边形．

（1）
如图1，在半对角四边形ABCD中，∠B＝ $\text{[math]}$ ∠D，∠C＝ $\text{[math]}$ ∠A，求∠B与∠C的度数之和；

（2）
如图2，锐角△ABC内接于⊙O，若边AB上存在一点D，使得BD＝BO．∠OBA的平分线交OA于点E，连结DE并延长交AC于点F，∠AFE＝2∠EAF．
求证：四边形DBCF是半对角四边形；

（3）
如图3，在（2）的条件下，过点D作DG⊥OB于点H，交BC于点G．当DH＝BG时，求△BGH与△ABC的面积之比．

查看解析收藏纠错

+选题

6.
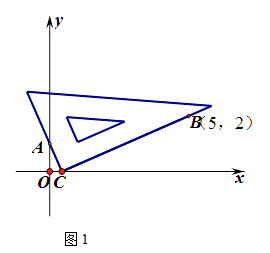
在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根，比如对于方程 $\text{[math]}$ ，操作步骤是：
第一步：根据方程系数特征，确定一对固定点A（0，1），B（5，2）；
第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A，另一条直角边恒过点B；
第三步：在移动过程中，当三角板的直角顶点落在x轴上点C处时，点C 的横坐标m即为该方程的一个实数根（如图1）
第四步：调整三角板直角顶点的位置，当它落在x轴上另一点D处时，点D 的横坐标为n即为该方程的另一个实数根。

（1）在图2 中，按照“第四步“的操作方法作出点D（请保留作出点D时直角三角板两条直角边的痕迹）

（2）结合图1，请证明“第三步”操作得到的m就是方程 $\text{[math]}$ 的一个实数根；

（3）上述操作的关键是确定两个固定点的位置，若要以此方法找到一元二次方程 $\text{[math]}$ 的实数根，请你直接写出一对固定点的坐标；

（4）实际上，（3）中的固定点有无数对，一般地，当 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与a，b，c之间满足怎样的关系时，点P（ $\text{[math]}$ ， $\text{[math]}$ ），Q（ $\text{[math]}$ ， $\text{[math]}$ ）就是符合要求的一对固定点？

查看解析收藏纠错

+选题

7.
如图1，已知▱ABCD，AB//x轴，AB=6，点A的坐标为（1，-4），点D的坐标为（-3，4），点B在第四象限，点P是▱ABCD边上的一个动点.

（1）若点P在边BC上，PD=CD，求点P的坐标.

（2）若点P在边AB，AD上，点P关于坐标轴对称的点Q落在直线y=x-1上，求点P的坐标.

（3）若点P在边AB，AD，CD上，点G是AD与y轴的交点，如图2，过点P作y轴的平行线PM，过点G作x轴的平行线GM，它们相交于点M，将△PGM沿直线PG翻折，当点M的对应点落在坐标轴上时，求点P的坐标（直接写出答案）.

查看解析收藏纠错

+选题

8.
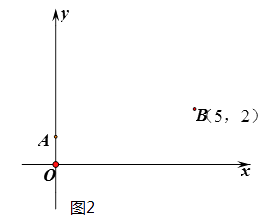
如图1，在平面直角坐标系中，四边形OABC各顶点的坐标分别O(0，0)，A(3，3 $\text{[math]}$ )，B(9，5 $\text{[math]}$ )，C(14，0).动点P与Q同时从O点出发，运动时间为t秒，点P沿OC方向以1单位长度/秒的速度向点C运动，点Q沿折线OA−AB−BC运动，在OA，AB，BC上运动的速度分别为3， $\text{[math]}$ ， $\text{[math]}$ (单位长度/秒)﹒当P，Q中的一点到达C点时，两点同时停止运动．

（1）求AB所在直线的函数表达式.

（2）如图2，当点Q在AB上运动时，求△CPQ的面积S关于t的函数表达式及S的最大值.

（3）在P，Q的运动过程中，若线段PQ的垂直平分线经过四边形OABC的顶点，求相应的t值.

查看解析收藏纠错

+选题
9.
如图，某日的钱塘江观潮信息如表：
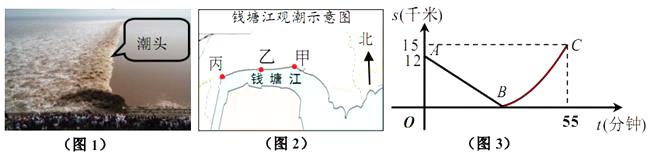
按上述信息，小红将“交叉潮”形成后潮头与乙地之间的距离 $\text{[math]}$ （千米）与时间 $\text{[math]}$ （分钟）的函数关系用图3表示，其中：“11：40时甲地‘交叉潮’的潮头离乙地12千米”记为点 $\text{[math]}$ ，点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，曲线 $\text{[math]}$ 可用二次函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 是常数）刻画．

（1）求 $\text{[math]}$ 的值，并求出潮头从甲地到乙地的速度；

（2） 11：59时，小红骑单车从乙地出发，沿江边公路以 $\text{[math]}$ 千米/分的速度往甲地方向去看潮，问她几分钟后与潮头相遇？

（3）相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为 $\text{[math]}$ 千米/分，小红逐渐落后，问小红与潮头相遇到落后潮头1.8千米共需多长时间？（潮水加速阶段速度 $\text{[math]}$ ， $\text{[math]}$ 是加速前的速度）．

查看解析收藏纠错

+选题
10.
如图，在平面直角坐标系 $\text{[math]}$ 中，已知 $\text{[math]}$ ， $\text{[math]}$ 两点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是线段 $\text{[math]}$ 上一点（与 $\text{[math]}$ ， $\text{[math]}$ 点不重合），抛物线 $\text{[math]}$ $\text{[math]}$ （ $\text{[math]}$ ）经过点 $\text{[math]}$ ， $\text{[math]}$ ，顶点为 $\text{[math]}$ ，抛物线 $\text{[math]}$ $\text{[math]}$ （ $\text{[math]}$ ）经过点 $\text{[math]}$ ， $\text{[math]}$ ，顶点为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的延长线相交于点 $\text{[math]}$ ．

（1）若 $\text{[math]}$ ， $\text{[math]}$ ，求抛物线 $\text{[math]}$ ， $\text{[math]}$ 的解析式；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值；

（3）是否存在这样的实数 $\text{[math]}$ （ $\text{[math]}$ ），无论 $\text{[math]}$ 取何值，直线 $\text{[math]}$ 与 $\text{[math]}$ 都不可能互相垂直？若存在，请直接写出 $\text{[math]}$ 的两个不同的值；若不存在，请说明理由．

查看解析收藏纠错

+选题