2017年河北省唐山市路北区中考数学二模试卷

修改时间：2024-07-12 浏览次数：437 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. ﹣2的绝对值是（）

A . 2 B . -2 C . $\text{[math]}$ D . 4

查看解析收藏纠错

+选题
2. 4的平方根是（）

A . 2 B . ﹣2 C . ±2 D . 16

查看解析收藏纠错

+选题
3. 下列运算正确的是（）

A . 5m+2m=7m² B . ﹣2m²•m³=2m⁵ C . （﹣a²b）³=﹣a⁶b³ D . （b+2a）（2a﹣b）=b²﹣4a²

查看解析收藏纠错

+选题
4. 下列图形中，能确定∠1＞∠2的是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 由若干个相同的小正方体搭成的一个几何体的俯视图如图，小正方形中的数字表示该位置的小正方体的个数，则这个几何体的主视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
6. 下列多边形中，内角和是外角和的两倍的是（）

A . 四边形 B . 五边形 C . 六边形 D . 八边形

查看解析收藏纠错

+选题
7. 计算（﹣1000 $\text{[math]}$ ）×（5﹣10）之值为何？（）

A . 1000 B . 1001 C . 4999 D . 5001

查看解析收藏纠错

+选题
8. 已知圆锥的侧面积为15π，底面半径为3，则圆锥的高为（）

A . 3 B . 4 C . 5 D . 7

查看解析收藏纠错

+选题
9. 已知关于x的分式方程 $\text{[math]}$ + $\text{[math]}$ =1的解是非负数，则m的取值范围是（）

A . m＞2 B . m≥2 C . m≥2且m≠3 D . m＞2且m≠3

查看解析收藏纠错

+选题
10. 如图为平面上圆O与四条直线l₁、l₂、l₃、l₄的位置关系．若圆O的半径为20公分，且O点到其中一直线的距离为14公分，则此直线为何？（）

A . l₁ B . l₂ C . l₃ D . l₄

查看解析收藏纠错

+选题
11. 学校为了丰富学生课余活动开展了一次“校园歌手大奖赛”的歌咏比赛，共有18名同学入围，他们的决赛成绩如下表：
成绩（分）
9.40
9.50
9.60
9.70
9.80
9.90
人数
2
3
5
4
3
1
则入围同学决赛成绩的中位数和众数分别是（　　）

A . 9.70，9.60 B . 9.60，9.60 C . 9.60，9.70 D . 9.65，9.60

查看解析收藏纠错

+选题
12. 如图，直角三角形ABC有一外接圆，其中∠B=90°，AB＞BC，今欲在 $\text{[math]}$ 上找一点P，使得 $\text{[math]}$ = $\text{[math]}$ ，以下是甲、乙两人的作法：
甲：⑴取AB中点D
    ⑵过D作直线AC的平行线，交 $\text{[math]}$ 于P，则P即为所求
乙：⑴取AC中点E
    ⑵过E作直线AB的平行线，交 $\text{[math]}$ 于P，则P即为所求
对于甲、乙两人的作法，下列判断何者正确？（   ）

A . 两人皆正确 B . 两人皆错误 C . 甲正确，乙错误C D . 甲错误，乙正确

查看解析收藏纠错

+选题
13. 如图，△ABC中，D为AB中点，E在AC上，且BE⊥AC．若DE=10，AE=16，则BE的长度为何？（）

A . 10 B . 11 C . 12 D . 13

查看解析收藏纠错

+选题
14. 小明原有300元，如图记录了他今天所有支出，其中饼干支出的金额被涂黑．若每包饼干的售价为13元，则小明可能剩下多少元？（）

A . 4 B . 14 C . 24 D . 34

查看解析收藏纠错

+选题
15. 如图，二次函数y=x²+bx+c的图象过点B（0，﹣2）．它与反比例函数y=﹣ $\text{[math]}$ 的图象交于点A（m，4），则这个二次函数的解析式为（）

A . y=x²﹣x﹣2 B . y=x²﹣x+2 C . y=x²+x﹣2 D . y=x²+x+2

查看解析收藏纠错

+选题
16. 如图，边长12的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF=3，则小正方形的边长为何？（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 5 D . 6

查看解析收藏纠错

+选题

二、填空题

17. 计算：（ $\text{[math]}$ +1）（3﹣ $\text{[math]}$ ）=．

查看解析收藏纠错

+选题
18. 如图，某数学兴趣小组为了测量河对岸l₁的两棵古树A、B之间的距离，他们在河这边沿着与AB平行的直线l₂上取C、D两点，测得∠ACB=15°，∠ACD=45°，若l₁、l₂之间的距离为50m，则古树A、B之间的距离为 m．

查看解析收藏纠错

+选题
19. 如图，在边长为1的正方形ABCD中，动点F，E分别以相同的速度从D，C两点同时出发向C和B运动（任何一个点到达即停止），过点P作PM∥CD交BC于M点，PN∥BC交CD于N点，连接MN，在运动过程中，
①AE和BF的位置关系为；
②线段MN的最小值为．

查看解析收藏纠错

+选题

三、解答题

20. 综合题。

（1）计算：（π﹣ $\text{[math]}$ ）⁰+ $\text{[math]}$ +（﹣1）²⁰¹³﹣ $\text{[math]}$ tan60°；

（2）先化简，再求值：（a+3）²+a（4﹣a），其中a为（1）中计算的结果．

查看解析收藏纠错

+选题
21. 如图，四边形ABCD是平行四边形，E、F是对角线BD上的点，∠1=∠2．

（1）求证：BE=DF；

（2）求证：AF∥CE．

查看解析收藏纠错

+选题
22. 某校举办一项小制作评比，作品上交时限为5月1日至30日，组委会把同学们交来的作品按时间顺序每5天组成一组，对每一组的件数进行统计，绘制成如图所示的统计图．已知从左到右各矩形的高度比为2：3：4：6：4：1．第三组的频数是12．
请你回答：

（1）本次活动共有件作品参赛；

（2）若将各组所占百分比绘制成扇形统计图，那么第四组对应的扇形的圆心角是度．

（3）本次活动共评出2个一等奖和3个二等奖及三等奖、优秀奖若干名，对一、二等奖作品进行编号并制作成背面完全一致的卡片，背面朝上的放置，随机抽出两张卡片，用列表法或树状图求抽到的作品恰好一个是一等奖，一个是二等奖的概率是多少？

查看解析收藏纠错

+选题
23. 甲、乙两支清雪队同时开始清理某路段积雪，一段时间后，乙队被调往别处，甲队又用了3小时完成了剩余的清雪任务，已知甲队每小时的清雪量保持不变，乙队每小时清雪50吨，甲、乙两队在此路段的清雪总量y（吨）与清雪时间x（时）之间的函数图象如图所示．

（1）乙队调离时，甲、乙两队已完成的清雪总量为吨；

（2）求此次任务的清雪总量m；

（3）求乙队调离后y与x之间的函数关系式．

查看解析收藏纠错

+选题
24. 如图，在⊙O中，AB是直径，点D是⊙O上一点且∠BOD=60°，过点D作⊙O的切线CD交AB的延长线于点C，E为 $\text{[math]}$ 的中点，连接DE，EB．

（1）求证：四边形BCDE是平行四边形；

（2）已知图中阴影部分面积为6π，求⊙O的半径r．

查看解析收藏纠错

+选题
25.
如图，已知点B（1，3），C（1，0），直线y=x+k经过点B，且与x轴交于点A，将△ABC沿直线AB折叠得到△ABD．

（1）填空：A点坐标为（，），D点坐标为（，）；

（2）若抛物线y= $\text{[math]}$ x²+bx+c经过C，D两点，求抛物线的解析式；

（3）将（2）中的抛物线沿y轴向上平移，设平移后所得抛物线与y轴交点为E，点M是平移后的抛物线与直线AB的公共点，在抛物线平移过程中是否存在某一位置使得直线EM∥x轴．若存在，此时抛物线向上平移了几个单位？若不存在，请说明理由．
（提示：抛物线y=ax²+bx+c（a≠0）的对称轴是x=﹣ $\text{[math]}$ ，顶点坐标是（﹣ $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
26.
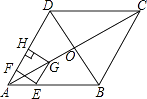
如图，在菱形ABCD中，对角线AC与BD相交于点O，AB=8，∠BAD=60°，点E从点A出发，沿AB以每秒2个单位长度的速度向终点B运动，当点E不与点A重合时，过点E作EF⊥AD于点F，作EG∥AD交AC于点G，过点G作GH⊥AD交AD（或AD的延长线）于点H，得到矩形EFHG，设点E运动的时间为t秒

（1）求线段EF的长（用含t的代数式表示）；

（2）求点H与点D重合时t的值；

（3）设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位，求S与t之间的函数关系式；

（4）矩形EFHG的对角线EH与FG相交于点O′，当OO′∥AD时，t的值为；当OO′⊥AD时，t的值为．

查看解析收藏纠错

+选题

成绩（分）	9.40	9.50	9.60	9.70	9.80	9.90
人数	2	3	5	4	3	1

2017年河北省唐山市路北区中考数学二模试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨