修改时间:2024-07-12 浏览次数:1184 类型:中考模拟
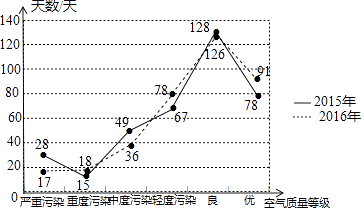
AQI是空气质量指数(Air Quality Index)的简称,是描述空气质量状况的指数.其数值越大说明空气污染状况越严重,对人体的健康危害也就越大.AQI共分六级,空气污染指数为0﹣50一级优,51﹣100二级良,101﹣150三级轻度污染,151﹣200四级中度污染,201﹣300五级重度污染,大于300六级严重污染.小明查阅了2015年和2016年某市全年的AQI指数,并绘制了如下统计图,并得出以下结论:①2016年重度污染的天数比2015年有所减少;②2016年空气质量优良的天数比2015年有所增加;③2015年和2016年AQI指数的中位数都集中在51﹣100这一档中;④2016年中度污染的天数比2015年多13天.以上结论正确的是( )
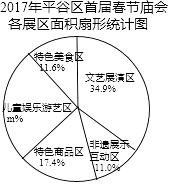
2017年1月28日至2月1日农历正月初一至初五,平谷区政府在占地面积6万平方米的琴湖公园举办主题为“逛平谷庙会乐百姓生活”的平谷区首届春节庙会.
本次庙会共设置了文艺展演区、非遗展示互动区、特色商品区、儿童娱乐游艺区、特色美食区等五个不同主题的展区.展区总面积1720平方米.文艺展演区占地面积600平方米,占展区总面积的34.9%;非遗展示区占地190平方米,占展区总面积的11.0%;特色商品区占地面积是文艺展演区的一半,占展区总面积的17.4%;特色美食区占地200平方米,占展区总面积的11.6%;还有孩子们喜爱的儿童娱乐游艺区.
此次庙会本着弘扬、挖掘、展示平谷春节及民俗文化,以京津冀不同地域的特色文化为出发点,全面展示平谷风土人情及津冀人文特色.大年初一,来自全国各地的约3.2万人踏着新春的脚步,揭开了首届平谷庙会的帷幕.大年初二尽管天气寒冷,市民逛庙会热情不减,又约有4.3万人次参观了庙会,品尝特色美食,观看绿都古韵、秧歌表演、天桥绝活,一路猜灯谜、赏图片展,场面火爆.琳琅满目的泥塑、木版画、剪纸、年画等民俗作品也让游客爱不释手,纷纷购买.大年初三,单日接待游客约4万人次,大年初四风和日丽的天气让庙会进入游园高峰,单日接待量较前日增长了约50%.大年初五,活动进入尾声,但庙会现场仍然人头攒动,仍约有5.5万人次来园参观.
小军根据学习函数的经验,对函数y=﹣ +|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
|
x |
﹣2 |
﹣1.9 |
﹣1.5 |
﹣1 |
﹣0.5 |
0 |
1 |
2 |
3 |
4 |
… |
|
y |
2 |
1.60 |
0.80 |
0 |
﹣0.72 |
﹣1.41 |
﹣0.37 |
0 |
0.76 |
1.55 |
… |
在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
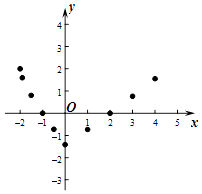
在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.

想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;
想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;
想法3:由等腰三角形三线合一,可得AD是∠BAC的角平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF….
请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);
试题篮