2017年湖北省襄阳市宜城市中考数学模拟试卷（5月份）

1. ﹣2的倒数的绝对值（）

A . ﹣2 B . 2 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图，AD是∠EAC的平分线，AD∥BC，∠B=35°，则∠C的度数为（）

A . 55° B . 45° C . 35° D . 25°

查看解析收藏纠错

+选题
3. 下列运算结果为m⁶的是（）

A . m²+m³ B . m²•m³ C . （﹣m²）³ D . m⁹÷m³

查看解析收藏纠错

+选题
4. 过度包装既浪费资源又污染环境，据测算，如果全国每年减少十分之一的包装纸用量，那么能减少3120000吨二氧化碳的排放量，把数据3120000用科学记数法表示为（）

A . 312×10⁴ B . 0.312×10⁷ C . 3.12×10⁶ D . 3.12×10⁷

查看解析收藏纠错

+选题
5. 如图，是某几何体的三视图及相关数据，则该几何体的表面积是（）

A . 39π B . 29π C . 24π D . 19π

查看解析收藏纠错

+选题
6. 有11名同学参加传统文化比赛，他们的预赛成绩各不相同，现取其中前5名参加决赛，小红同学在知道自己成绩的情况下，要判断自己能否进入决赛，还需要知道这11名同学成绩的（）

A . 方差 B . 平均数 C . 众数 D . 中位数

查看解析收藏纠错

+选题
7. 某单位组织34人分别到张自忠将军纪念园和烈士陵园进行革命传统教育，到张自忠将军纪念园的人数是到烈士陵园的人数的2倍多1人，求到两地的人数各是多少？设到张自忠将军纪念园的人数为x人，到烈士陵园的人数为y人．下面所列的方程组正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，要说明∠D′O′C′=∠DOC，需要证明△D′O′C′≌△DOC，则这两个三角形全等的依据是（）

A . 边边边 B . 边角边 C . 角边角 D . 角角边

查看解析收藏纠错

+选题
9. 如图，已知AB是⊙O的直径，∠CAB=50°，则∠D的度数为（）

A . 20° B . 40° C . 50° D . 70°

查看解析收藏纠错

+选题
10. 在同一坐标系中一次函数y=ax﹣b和二次函数y=ax²+bx的图象可能为（）

A . B . C . D .

查看解析收藏纠错

+选题

11. 方程 $\text{[math]}$ =1的根是x=．

查看解析收藏纠错

+选题
12. 若函数y=（m+1）x^|^m^|是正比例函数，则该函数的图象经过第象限．

查看解析收藏纠错

+选题
13. 小明用S²= $\text{[math]}$ [（x₁﹣5）²+（x₂﹣5）²+…+（x₁₀﹣5）²]计算一组数据的方差，那么x₁+x₂+x₃+…+x₁₀=．

查看解析收藏纠错

+选题
14. 若实数x、y满足|x﹣5|+ $\text{[math]}$ =0，则以x、y的值为边长的等腰三角形的周长为．

查看解析收藏纠错

+选题
15. 如图，将△ABC沿BC方向平移3cm得到△DEF，若四边形ABFD的周长为22cm，则△ABC的周长为 cm．

查看解析收藏纠错

+选题
16. 如图，△ABC中，∠C=90°，AC=6，AB=10，D为BC边的中点，以AD上一点O为圆心的⊙O和AB、BC均相切，则⊙O的半径为．

查看解析收藏纠错

+选题

17. 先化简，再求值：（ $\text{[math]}$ ﹣ $\text{[math]}$ ）÷ $\text{[math]}$ ，其中x满足方程x²﹣4x﹣2013=0．

查看解析收藏纠错

+选题
18. 为了巩固全国文明城市建设成果，突出城市品质的提升，近年来，某市积极落实节能减排政策，推行绿色建筑，据统计，该市2014年的绿色建筑面积约为700万平方米，2016年达到了1183万平方米．若2015年、2016年的绿色建筑面积按相同的增长率逐年递增，请解答下列问题：

（1）求这两年该市推行绿色建筑面积的年平均增长率；

（2） 2017年该市计划推行绿色建筑面积达到1500万平方米．如果2017年仍保持相同的年平均增长率，请你预测2017年该市能否完成计划目标？

查看解析收藏纠错

+选题
19. 某条道路上通行车辆限速为60千米/时，在离道路50米的点P处建一个监测点，道路AB段为检测区（如图）．在△ABP中，已知∠PAB=30°，∠PBA=45°，一辆轿车通过AB段的时间8.1秒，请判断该车是否超速？（参考数据： $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73，60千米/时= $\text{[math]}$ 米/秒）

查看解析收藏纠错

+选题
20.
“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：

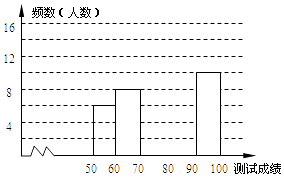
组别
成绩x分
频数（人数）
第1组
50≤x＜60
6
第2组
60≤x＜70
8
第3组
70≤x＜80
14
第4组
80≤x＜90
a
第5组
90≤x＜100
10
请结合图表完成下列各题：

（1） ①表中a的值为；②频数分布直方图补充完整；

（2）若测试成绩不低于80分为优秀，则本次测试的优秀率是．

（3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．

查看解析收藏纠错

+选题
21. 已知，在平面直角坐标系xOy中，点A在x轴负半轴上，点B在y轴正半轴上，OA=OB，函数y=﹣ $\text{[math]}$ 的图象与线段AB交于M点，且AM=BM．

（1）求点M的坐标；

（2）求直线AB的解析式．

查看解析收藏纠错

+选题
22. 如图，在△ABC中，∠ABC=90°，D是边AC上的一点，连接BD，使∠A=2∠1，E是BC上的一点，以BE为直径的⊙O经过点D．

（1）求证：AC是⊙O的切线；

（2）若∠A=60°，⊙O的半径为2，求阴影部分的面积．（结果保留根号和π）

查看解析收藏纠错

+选题
23. 某厂家生产的一种新型节能灯，为了打开市场出台了相关政策：由厂家协调，厂家按成本价提供产品给经营户自主销售，成本价与出厂价之间的差价由厂家承担．李明按照相关政策投资销售本产品．已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数：y=﹣10x+500．

（1）李明在开始销售的第一个月将销售单价定为20元，那么厂家这个月为他承担的总差价为多少元？

（2）设李明获得的利润为w（元），当销售单价定为多少元时，每月可获得最大利润？

（3）物价部门规定，这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元，那么厂家为他承担的总差价最少为多少元？

查看解析收藏纠错

+选题
24.
如图，在正方形ABCD中，点E是AD上的点，点F是BC的延长线上一点，CF=DE，连结BE和EF，EF与CD交于点G，且∠FBE=∠FEB．

（1）过点F作FH⊥BE于点H，证明： $\text{[math]}$ = $\text{[math]}$ ；

（2）猜想：BE、AE、EF之间的数量关系，并证明你的结论；

（3）若DG=2，求AE值．

查看解析收藏纠错

+选题
25.
如图，抛物线y=ax²+b与x轴交于点A、B，且A点的坐标为（1，0），与y轴交于点C（0，1）．

（1）求抛物线的解析式，并求出点B坐标；

（2）过点B作BD∥CA交抛物线于点D，连接BC、CA、AD，求四边形ABCD的周长；（结果保留根号）

（3）在x轴上方的抛物线上是否存在点P，过点P作PE垂直于x轴，垂足为点E，使以B、P、E为顶点的三角形与△CBD相似？若存在请求出P点的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题

2017年湖北省襄阳市宜城市中考数学模拟试卷（5月份）

一、选择题

二、填空题

三、解答题

相关试卷收起∨

组别	成绩x分	频数（人数）
第1组	50≤x＜60	6
第2组	60≤x＜70	8
第3组	70≤x＜80	14
第4组	80≤x＜90	a
第5组	90≤x＜100	10

2017年湖北省襄阳市宜城市中考数学模拟试卷（5月份）

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨