2017年贵州省遵义市中考数学试卷

修改时间：2024-07-12 浏览次数：1578 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. ﹣3的相反数是（）

A . ﹣3 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 2017年遵义市固定资产总投资计划为2580亿元，将2580亿元用科学记数法表示为（）

A . 2.58×10¹¹ B . 2.58×10¹² C . 2.58×10¹³ D . 2.58×10¹⁴

查看解析收藏纠错

+选题
3. 把一张长方形纸片按如图①，图②的方式从右向左连续对折两次后得到图③，再在图③中挖去一个如图所示的三角形小孔，则重新展开后得到的图形是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 下列运算正确的是（）

A . 2a⁵﹣3a⁵=a⁵ B . a²•a³=a⁶ C . a⁷÷a⁵=a² D . （a²b）³=a⁵b³

查看解析收藏纠错

+选题
5. 我市连续7天的最高气温为：28°，27°，30°，33°，30°，30°，32°，这组数据的平均数和众数分别是（）

A . 28°，30° B . 30°，28° C . 31°，30° D . 30°，30°

查看解析收藏纠错

+选题
6. 把一块等腰直角三角尺和直尺如图放置，如果∠1=30°，则∠2的度数为（）

A . 45° B . 30° C . 20° D . 15°

查看解析收藏纠错

+选题
7. 不等式6﹣4x≥3x﹣8的非负整数解为（）

A . 2个 B . 3个 C . 4个 D . 5个

查看解析收藏纠错

+选题
8. 已知圆锥的底面积为9πcm² ，母线长为6cm，则圆锥的侧面积是（）

A . 18πcm² B . 27πcm² C . 18cm² D . 27cm²

查看解析收藏纠错

+选题
9. 关于x的一元二次方程x²+3x+m=0有两个不相等的实数根，则m的取值范围为（）

A . m≤ $\text{[math]}$ B . m $\text{[math]}$ C . m≤ $\text{[math]}$ D . m $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，△ABC的面积是12，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是（）

A . 4.5 B . 5 C . 5.5 D . 6

查看解析收藏纠错

+选题
11. 如图，抛物线y=ax²+bx+c经过点（﹣1，0），对称轴l如图所示，则下列结论：①abc＞0；②a﹣b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（）

A . ①③ B . ②③ C . ②④ D . ②③④

查看解析收藏纠错

+选题
12.
如图，△ABC中，E是BC中点，AD是∠BAC的平分线，EF//AD交AC于F．若AB=11，AC=15，则FC的长为（）

A . 11 B . 12 C . 13 D . 14

查看解析收藏纠错

+选题

二、填空题

13. 计算： $\text{[math]}$ =．

查看解析收藏纠错

+选题
14. 一个正多边形的一个外角为30°，则它的内角和为．

查看解析收藏纠错

+选题
15. 按一定规律排列的一列数依次为： $\text{[math]}$ ，1， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，…，按此规律，这列数中的第100个数是．

查看解析收藏纠错

+选题
16. 明代数学家程大位的《算法统宗》中有这样一个问题（如图），其大意为：有一群人分银子，如果每人分七两，则剩余四两；如果每人分九两，则还差八两，请问：所分的银子共有两．（注：明代时1斤=16两，故有“半斤八两”这个成语）

查看解析收藏纠错

+选题
17. 如图，AB是⊙O的直径，AB=4，点M是OA的中点，过点M的直线与⊙O交于C，D两点．若∠CMA=45°，则弦CD的长为．

查看解析收藏纠错

+选题
18.
如图，点E，F在函数y= $\text{[math]}$ 的图象上，直线EF分别与x轴、y轴交于点A、B，且BE：BF=1：3，则△EOF的面积是．

查看解析收藏纠错

+选题

三、解答题

19. 计算：|﹣2 $\text{[math]}$ |+（4﹣π）⁰﹣ $\text{[math]}$ +（﹣1）^﹣²⁰¹⁷ ．

查看解析收藏纠错

+选题
20. 化简分式：（ $\text{[math]}$ ﹣ $\text{[math]}$ ）÷ $\text{[math]}$ ，并从1，2，3，4这四个数中取一个合适的数作为x的值代入求值．

查看解析收藏纠错

+选题
21. 学校召集留守儿童过端午节，桌上摆有甲、乙两盘粽子，每盘中盛有白粽2个，豆沙粽1个，肉粽1个（粽子外观完全一样）．

（1）小明从甲盘中任取一个粽子，取到豆沙粽的概率是；

（2）小明在甲盘和乙盘中先后各取了一个粽子，请用树状图或列表法求小明恰好取到两个白粽子的概率．

查看解析收藏纠错

+选题
22.
乌江快铁大桥是快铁渝黔线的一项重要工程，由主桥AB和引桥BC两部分组成（如图所示），建造前工程师用以下方式做了测量；无人机在A处正上方97m处的P点，测得B处的俯角为30°（当时C处被小山体阻挡无法观测），无人机飞行到B处正上方的D处时能看到C处，此时测得C处俯角为80°36′．
（长度均精确到1m，参考数据： $\text{[math]}$ ≈1.73，sin80°36′≈0.987，cos80°36′≈0.163，tan80°36′≈6.06）

（1）求主桥AB的长度；

（2）若两观察点P、D的连线与水平方向的夹角为30°，求引桥BC的长．

查看解析收藏纠错

+选题
23. 贵州省是我国首个大数据综合试验区，大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值，为创建大数据应用示范城市，我市某机构针对市民最关心的四类生活信息进行了民意调查（被调查者每人限选一项），下面是部分四类生活信息关注度统计图表，请根据图中提供的信息解答下列问题：

（1）本次参与调查的人数有人；

（2）关注城市医疗信息的有人，并补全条形统计图；

（3）扇形统计图中，D部分的圆心角是度；

（4）说一条你从统计图中获取的信息．

查看解析收藏纠错

+选题
24. 如图，PA、PB是⊙O的切线，A、B为切点，∠APB=60°，连接PO并延长与⊙O交于C点，连接AC，BC．

（1）求证：四边形ACBP是菱形；

（2）若⊙O半径为1，求菱形ACBP的面积．

查看解析收藏纠错

+选题
25. 为厉行节能减排，倡导绿色出行，今年3月以来．“共享单车”（俗称“小黄车”）公益活动登陆我市中心城区，某公司拟在甲、乙两个街道社区投放一批“小黄车”，这批自行车包括A、B两种不同款型，请回答下列问题：

问题1：单价
该公司早期在甲街区进行了试点投放，共投放A、B两型自行车各50辆，投放成本共计7500元，其中B型车的成本单价比A型车高10元，A、B两型自行车的单价各是多少？

问题2：投放方式
该公司决定采取如下投放方式：甲街区每1000人投放a辆“小黄车”，乙街区每1000人投放 $\text{[math]}$ 辆“小黄车”，按照这种投放方式，甲街区共投放1500辆，乙街区共投放1200辆，如果两个街区共有15万人，试求a的值．

查看解析收藏纠错

+选题
26.
边长为2 $\text{[math]}$ 的正方形ABCD中，P是对角线AC上的一个动点（点P与A、C不重合），连接BP，将BP绕点B顺时针旋转90°到BQ，连接QP，QP与BC交于点E，QP延长线与AD（或AD延长线）交于点F．

（1）连接CQ，证明：CQ=AP；

（2）设AP=x，CE=y，试写出y关于x的函数关系式，并求当x为何值时，CE= $\text{[math]}$ BC；

（3）猜想PF与EQ的数量关系，并证明你的结论．

查看解析收藏纠错

+选题
27.
如图，抛物线y=ax²+bx﹣a﹣b（a＜0，a、b为常数）与x轴交于A、C两点，与y轴交于B点，直线AB的函数关系式为y= $\text{[math]}$ x+ $\text{[math]}$ ．

（1）求该抛物线的函数关系式与C点坐标；

（2）已知点M（m，0）是线段OA上的一个动点，过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点，当m为何值时，△BDE恰好是以DE为底边的等腰三角形？

（3）在（2）问条件下，当△BDE恰好是以DE为底边的等腰三角形时，动点M相应位置记为点M′，将OM′绕原点O顺时针旋转得到ON（旋转角在0°到90°之间）；
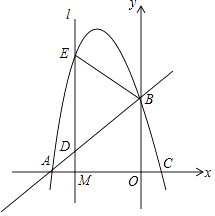
i：探究：线段OB上是否存在定点P（P不与O、B重合），无论ON如何旋转， $\text{[math]}$ 始终保持不变，若存在，试求出P点坐标；若不存在，请说明理由；
ii：试求出此旋转过程中，（NA+ $\text{[math]}$ NB）的最小值．

查看解析收藏纠错

+选题

2017年贵州省遵义市中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨