2017年山东省烟台市中考数学试卷

修改时间：2024-07-12 浏览次数：2361 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 下列实数中的无理数是（）

A . $\text{[math]}$ B . π C . 0 D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列国旗图案是轴对称图形但不是中心对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 我国推行“一带一路”政策以来，已确定沿线有65个国家加入，共涉及总人口约达46亿人，用科学记数法表示该总人口为（）

A . 4.6×10⁹ B . 46×10⁸ C . 0.46×10¹⁰ D . 4.6×10¹⁰

查看解析收藏纠错

+选题
4. 如图所示的工件，其俯视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 某城市几条道路的位置关系如图所示，已知AB∥CD，AE与AB的夹角为48°，若CF与EF的长度相等，则∠C的度数为（）

A . 48° B . 40° C . 30° D . 24°

查看解析收藏纠错

+选题
6. 如图，若用我们数学课本上采用的科学计算器进行计算，其按键顺序如下：
则输出结果应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7.
用棋子摆出下列一组图形：
按照这种规律摆下去，第n个图形用的棋子个数为（）

A . 3n B . 6n C . 3n+6 D . 3n+3

查看解析收藏纠错

+选题
8.
甲、乙两地去年12月前5天的日平均气温如图所示，下列描述错误的是（）

A . 两地气温的平均数相同 B . 甲地气温的中位数是6℃ C . 乙地气温的众数是4℃ D . 乙地气温相对比较稳定

查看解析收藏纠错

+选题
9. 如图，▱ABCD中，∠B=70°，BC=6，以AD为直径的⊙O交CD于点E，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ π B . $\text{[math]}$ π C . $\text{[math]}$ π D . $\text{[math]}$ π

查看解析收藏纠错

+选题
10. 若x₁ ， x₂是方程x²﹣2mx+m²﹣m﹣1=0的两个根，且x₁+x₂=1﹣x₁x₂ ，则m的值为（）

A . ﹣1或2 B . 1或﹣2 C . ﹣2 D . 1

查看解析收藏纠错

+选题
11. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，对称轴是直线x=1，下列结论：
①ab＜0；②b²＞4ac；③a+b+2c＜0；④3a+c＜0．
其中正确的是（）

A . ①④ B . ②④ C . ①②③ D . ①②③④

查看解析收藏纠错

+选题
12.
如图，数学实践活动小组要测量学校附近楼房CD的高度，在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°，向前走20米到达A′处，测得点D的仰角为67.5°，已知测倾器AB的高度为1.6米，则楼房CD的高度约为（结果精确到0.1米， $\text{[math]}$ ≈1.414）（）

A . 34.14米 B . 34.1米 C . 35.7米 D . 35.74米

查看解析收藏纠错

+选题

二、填空题

13. 3⁰×（ $\text{[math]}$ ）^﹣²+|﹣2|=．

查看解析收藏纠错

+选题
14. 在Rt△ABC中，∠C=90°，AB=2，BC= $\text{[math]}$ ，则sin $\text{[math]}$ =．

查看解析收藏纠错

+选题
15. 运行程序如图所示，从“输入实数x”到“结果是否＜18”为一次程序操作，
若输入x后程序操作仅进行了一次就停止，则x的取值范围是．

查看解析收藏纠错

+选题
16. 如图，在直角坐标系中，每个小方格的边长均为1，△AOB与△A′OB′是以原点O为位似中心的位似图形，且相似比为3：2，点A，B都在格点上，则点B′的坐标是．

查看解析收藏纠错

+选题
17. 如图，直线y=x+2与反比例函数y= $\text{[math]}$ 的图象在第一象限交于点P，若OP= $\text{[math]}$ ，则k的值为．

查看解析收藏纠错

+选题
18. 如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB．已知OA=6，取OA的中点C，过点C作CD⊥OA交 $\text{[math]}$ 于点D，点F是 $\text{[math]}$ 上一点．若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD，DF，FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为．

查看解析收藏纠错

+选题

三、解答题

19. 先化简，再求值：（x﹣ $\text{[math]}$ ）÷ $\text{[math]}$ ，其中x= $\text{[math]}$ ，y= $\text{[math]}$ ﹣1．

查看解析收藏纠错

+选题
20. 主题班会课上，王老师出示了如图所示的一幅漫画，经过同学们的一番热议，达成以下四个观点：
A．放下自我，彼此尊重； B．放下利益，彼此平衡；
C．放下性格，彼此成就； D．合理竞争，合作双赢．
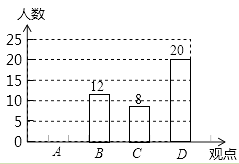
要求每人选取其中一个观点写出自己的感悟，根据同学们的选择情况，小明绘制了下面两幅不完整的图表，请根据图表中提供的信息，解答下列问题：
观点
频数
频率
A
a
0.2
B
12
0.24
C
8
b
D
20
0.4

（1）参加本次讨论的学生共有人；

（2）表中a=，b=；

（3）将条形统计图补充完整；

（4）现准备从A，B，C，D四个观点中任选两个作为演讲主题，请用列表或画树状图的方法求选中观点D（合理竞争，合作双赢）的概率．

查看解析收藏纠错

+选题
21. 今年，我市某中学响应习总书记“足球进校园”的号召，开设了“足球大课间”活动，现需要购进100个某品牌的足球供学生使用，经调查，该品牌足球2015年单价为200元，2017年单价为162元．

（1）求2015年到2017年该品牌足球单价平均每年降低的百分率；

（2）选购期间发现该品牌足球在两个文体用品商场有不同的促销方案：
试问去哪个商场购买足球更优惠？

查看解析收藏纠错

+选题
22. 数学兴趣小组研究某型号冷柜温度的变化情况，发现该冷柜的工作过程是：当温度达到设定温度﹣20℃时，制冷停止，此后冷柜中的温度开始逐渐上升，当上升到﹣4℃时，制冷开始，温度开始逐渐下降，当冷柜自动制冷至﹣20℃时，制冷再次停止，…，按照以上方式循环进行．
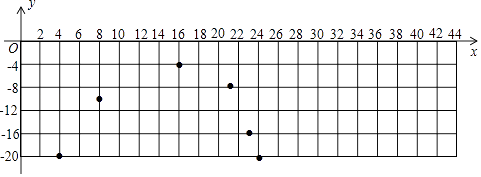
同学们记录了44min内15个时间点冷柜中的温度y（℃）随时间x（min）的变化情况，制成下表：
时间x/min
…
4
8
10
16
20
21
22
23
24
28
30
36
40
42
44
…
温度y/℃
…
﹣20
﹣10
﹣8
﹣5
﹣4
﹣8
﹣12
﹣16
﹣20
﹣10
﹣8
﹣5
﹣4
a
﹣20
…

（1）通过分析发现，冷柜中的温度y是时间x的函数．
①当4≤x＜20时，写出一个符合表中数据的函数解析式；
②当20≤x＜24时，写出一个符合表中数据的函数解析式；

（2） a的值为；

（3）如图，在直角坐标系中，已描出了上表中部分数据对应的点，请描出剩余数据对应的点，并画出当4≤x≤44时温度y随时间x变化的函数图象．

查看解析收藏纠错

+选题
23.

（1）
如图1，△ABC为等边三角形，现将三角板中的60°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于30°），旋转后三角板的一直角边与AB交于点D，在三角板斜边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=30°，连接AF，EF．
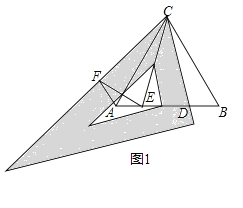
①求∠EAF的度数；
②DE与EF相等吗？请说明理由；

（2）
如图2，△ABC为等腰直角三角形，∠ACB=90°，先将三角板的90°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于45°），旋转后三角板的一直角边与AB交于点D，在三角板另一直角边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=45°，连接AF，EF，请直接写出探究结果：
①求∠EAF的度数；
②线段AE，ED，DB之间的数量关系．

查看解析收藏纠错

+选题
24. 如图，菱形ABCD中，对角线AC，BD相交于点O，AC=12cm，BD=16cm，动点N从点D出发，沿线段DB以2cm/s的速度向点B运动，同时动点M从点B出发，沿线段BA以1cm/s的速度向点A运动，当其中一个动点停止运动时另一个动点也随之停止，设运动时间为t（s）（t＞0），以点M为圆心，MB长为半径的⊙M与射线BA，线段BD分别交于点E，F，连接EN．

（1）求BF的长（用含有t的代数式表示），并求出t的取值范围；

（2）当t为何值时，线段EN与⊙M相切？

（3）若⊙M与线段EN只有一个公共点，求t的取值范围．

查看解析收藏纠错

+选题
25.
如图1，抛物线y=ax²+bx+2与x轴交于A，B两点，与y轴交于点C，AB=4，矩形OBDC的边CD=1，延长DC交抛物线于点E．

（1）求抛物线的解析式；

（2）
如图2，点P是直线EO上方抛物线上的一个动点，过点P作y轴的平行线交直线EO于点G，作PH⊥EO，垂足为H．设PH的长为l，点P的横坐标为m，求l与m的函数关系式（不必写出m的取值范围），并求出l的最大值；

（3）如果点N是抛物线对称轴上的一点，抛物线上是否存在点M，使得以M，A，C，N为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题

时间x/min	…	4	8	10	16	20	21	22	23	24	28	30	36	40	42	44	…
温度y/℃	…	﹣20	﹣10	﹣8	﹣5	﹣4	﹣8	﹣12	﹣16	﹣20	﹣10	﹣8	﹣5	﹣4	a	﹣20	…

观点	频数	频率
A	a	0.2
B	12	0.24
C	8	b
D	20	0.4

2017年山东省烟台市中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨