2017年四川省内江市资中县中考数学二模试卷

1. ﹣2017的倒数是（）

A . 2017 B . ﹣2017 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
2. 世界最大的500米口径球面射电望远镜（FAST）于2016年9月25日在贵州省平塘县落成启用，被誉为“中国天眼”，能够接收到137亿光年以外的电磁信号137亿用科学记数法表示为（）

A . 137×10⁸ B . 1.37×10⁹ C . 1.37×10¹⁰ D . 1.37×10¹¹

查看解析收藏纠错

+选题
3. 如图是由四个大小相同的正方体组成的几何体，那么它的主视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 下列运算正确的是（）

A . a⁶+a³=a⁹ B . a²•a³=a⁵ C . （2a）³=6a³ D . （a﹣b）²=a²﹣b²

查看解析收藏纠错

+选题
5. 如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB交于点E，则∠DEO的度数为（）

A . 85° B . 70° C . 75° D . 60°

查看解析收藏纠错

+选题
6. 若a＜b，则下列各式中，错误的是（）

A . a﹣3＜b﹣3 B . ﹣a＜﹣b C . ﹣2a＞﹣2b D . $\text{[math]}$ a＜ $\text{[math]}$ b

查看解析收藏纠错

+选题
7. 数据3，6，7，4，x的平均数是5，则这组数据的中位数是（）

A . 4 B . 4.5 C . 5 D . 6

查看解析收藏纠错

+选题
8. 已知P₁（x₁ ， y₁），P₂（x₂ ， y₂）是一次函数y=﹣ $\text{[math]}$ x+2图象上的两点，下列判断中，正确的是（）

A . y₁＞y₂ B . y₁＜y₂ C . 当x₁＜x₂时，y₁＜y₂ D . 当x₁＜x₂时，y₁＞y₂

查看解析收藏纠错

+选题
9. 如图，已知矩形ABCD中，R，P分别是DC、BC上的点，E，F分别是AP，RP的中点，当P在BC上从B向C移动而R不动时，那么下列结论成立的是（）

A . 线段EF的长逐渐增大 B . 线段EF的长逐渐减小 C . 线段EF的长不改变 D . 线段EF的长不能确定

查看解析收藏纠错

+选题
10. 甲车行驶30千米与乙车行驶40千米所用时间相同，已知乙车每小时比甲车多行驶15千米，设甲车的速度为x千米/小时，依据题意列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
11. 计算机是将信息转换成二进制数进行处理的，二进制即“逢2进1”，如（1101）₂表示二进制数，将它转换成十进制形式是1×2³+1×2²+0×2¹+1×2⁰=13，那么将二进制（1111）₂转换成十进制形式是（）

A . 8 B . 15 C . 30 D . 31

查看解析收藏纠错

+选题
12. 如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论：①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④S_△_ABC=S_四边形_AOCP ，其中正确的个数是（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题

13. 化简： $\text{[math]}$ =．

查看解析收藏纠错

+选题
14. 分解因式：x³﹣4x=．

查看解析收藏纠错

+选题
15. =在一个不透明的盒子中装有10个白球和若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出1个球，它恰好是白球的概率是 $\text{[math]}$ ，则该盒中黄球的个数为．

查看解析收藏纠错

+选题
16. 如图，在平面直角坐标系中有一正方形AOBC，反比例函数y= $\text{[math]}$ 经过正方形AOBC对角线的交点，半径为（6﹣3 $\text{[math]}$ ）的圆内切于△ABC，则k的值为．

查看解析收藏纠错

+选题

17. 计算：|1﹣ $\text{[math]}$ |+（π﹣2014）⁰﹣2sin45°+（ $\text{[math]}$ ）^﹣² ．

查看解析收藏纠错

+选题
18. 如图，在△ABC中，∠ABC=45°，AD、BE是△ABC的高，AD、BE相交于点F．
求证：BF=AC．

查看解析收藏纠错

+选题
19.
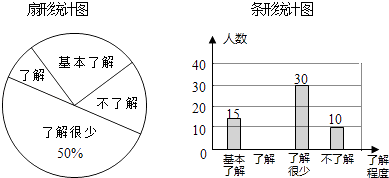
“校园安全”受到全社会的广泛关注，东营市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了如图两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：

（1）接受问卷调查的学生共有人，扇形统计图中“基本了解”部分所对应扇形的圆心角为；

（2）请补全条形统计图；

（3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数；

（4）若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．

查看解析收藏纠错

+选题
20.
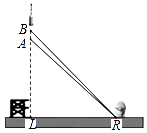
2016年11月3日，我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空，这标志着我国从航天大国迈向航天强国．如图，火箭从地面L处发射，当火箭到达A点时，从位于地面R处雷达站测得AR的距离是6km，仰角为42.4°；1秒后火箭到达B点，此时测得仰角为45.5°．

（1）求发射台与雷达站之间的距离LR；

（2）求这枚火箭从A到B的平均速度是多少？（结果精确到0.01，参考数据：sin42.4°≈0.67，cos42.4°≈0.74，tan42.4°≈0.905，sin45.5°≈0.71，cos45.5°≈0.70，tan45.5°≈1.02 ）

查看解析收藏纠错

+选题
21.
如图，在锐角△ABC中，BC=10，高AD=8，矩形EFPQ的一边QP在BC边上，E、F两点分别在AB、AC上，AD交EF于点H．

（1）求证： $\text{[math]}$ = $\text{[math]}$ ；

（2）设EF的长为x．
①当x为何值时，矩形EFPQ为正方形？
②当x为何值时，矩形EFPQ的面积最大？并求其最大值．

查看解析收藏纠错

+选题

22. 已知 $\text{[math]}$ ﹣ $\text{[math]}$ =3，则 $\text{[math]}$ =．

查看解析收藏纠错

+选题
23. 如图，在反比例函数y= $\text{[math]}$ （x＞0）的图象上，有点P₁ ， P₂ ， P₃ ， P₄ ， …，它们的横坐标依次为2，4，6，8，…分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次记为S₁ ， S₂ ， S₃ ， …，S_n ，则S₁+S₂+S₃+…+S_n=（用含n的代数式表示）

查看解析收藏纠错

+选题
24. 如图，△ABC中，∠C=90°，AC=6，AB=10，D为BC边的中点，以AD上一点O为圆心的⊙O和AB、BC均相切，则OD的长为．

查看解析收藏纠错

+选题
25. 如图，在边长为4的菱形ABCD中，∠A=60°，M是AD边的中点，点N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则线段A′C长度的最小值是．

查看解析收藏纠错

+选题

26. 某公司在甲地、乙地分别生产了17台、15台同一种型号的机械设备，现要将这些设备全部运往A、B两市，其中运往A市18台、运往B市14台，从甲地运往A、B两市的费用分别为800元/台和500元/台，从乙地运往A、B两市的费用分别为700元/台和600元/台．设甲地运往A市的设备有x台．

（1）请用x的代数式分别表示甲地运往B市、乙地运往A市、乙地运往B市的设备台数；

（2）求出总运费y（元）与x（台）的函数关系式，并求出自变量的取值范围；

（3）要使总运费不高于20200元，请你帮助该公司设计调配方案，并写出有哪几种方案，哪种方案总运费最小，最小值是多少？

查看解析收藏纠错

+选题
27.
如图，已知在△ABP中，C是BP边上一点，∠PAC=∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E．

（1）求证：PA是⊙O的切线；

（2）
过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AG•AB=12，求AC的长；

（3）在满足（2）的条件下，若AF：FD=1：2，GF=1，求⊙O的半径及sin∠ACE的值．

查看解析收藏纠错

+选题
28.
如图，抛物线y=ax²+bx+c（a≠0）与x轴、y轴分别交于A（﹣1，0）、B（3，0）、C（0，3）三点．

（1）试求抛物线的解析式；

（2） P是直线BC上方抛物线上的一个动点，设P的横坐标为t，P到BC的距离为h，求h与t的函数关系式，并求出h的最大值．

（3）设点M是x轴上的动点，在平面直角坐标系中，是否存在点N，使得以点A、C、M、N为顶点的四边形是菱形？若存在，求出所有符合条件的点N坐标；若不存在，说明理由．

查看解析收藏纠错

+选题

2017年四川省内江市资中县中考数学二模试卷

一、选择题

二、填空题

三、解答题

四、填空题

五、解答题

相关试卷收起∨

2017年四川省内江市资中县中考数学二模试卷

一、选择题

二、填空题

三、解答题

四、填空题

五、解答题

相关试卷 收起∨

相关试卷收起∨