修改时间:2024-07-13 浏览次数:617 类型:中考真卷
|
90 |
85 |
68 |
92 |
81 |
84 |
95 |
93 |
87 |
89 |
78 |
99 |
89 |
85 |
97 |
|
88 |
81 |
95 |
86 |
98 |
95 |
93 |
89 |
86 |
84 |
87 |
79 |
85 |
89 |
82 |
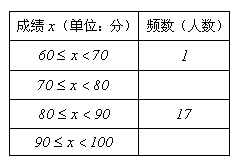
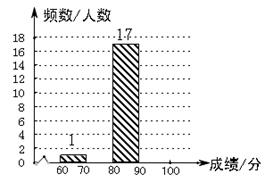
试题篮