河北省秦皇岛市暨海港区2018-2019学年中考数学二模考试试卷

修改时间：2024-07-13 浏览次数：691 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题（本大题共16个小题，共42分．1~10小题各3分，11~16小题各2分．）

1. 图是由相同的小正方体木块粘在一起的几何体，它的左视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
2. 把一个数写成ax10ⁿ（1≤a<10，n为整数）的形式为3.57×10^-5 ，则原数为（）

A . 0.0000357 B . 0.000357 C . 357000 D . 3570000

查看解析收藏纠错

+选题
3. 如图，是两个圆形转盘，同时旋转两个转盘，两个转盘的指针都落在“1”区域的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 下列图形中，表示南偏西30°的射线是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 如图，A、B两地之间有一池塘，要测量A、B两地之间的距离，选择一点O，连接AO并延长到点C，使OC= $\text{[math]}$ AO，连接BO并延长到点D，使OD= $\text{[math]}$ BO．测得C、D间距离为30米，则A、B两地之间的距离为（）

A . 30米 B . 45米 C . 60米 D . 90米

查看解析收藏纠错

+选题
6. 下列计算中，正确的是（）

A . $\text{[math]}$ =±2 B . 2+ $\text{[math]}$ =2 $\text{[math]}$ C . a²·a⁴=a⁸ D . (a³）²=a⁶

查看解析收藏纠错

+选题
7. 下列各数中，为不等式组 $\text{[math]}$ 的解的是（）

A . -1 B . 0 C . 2 D . 4

查看解析收藏纠错

+选题
8. 化简 $\text{[math]}$ 的结果是 $\text{[math]}$ ，则a的值是（）

A . 1 B . -1 C . 2 D . -2

查看解析收藏纠错

+选题
9. 甲、乙、丙、丁四名射击运动员参加了预选赛，他们的射击成绩的平均环数 $\text{[math]}$ 及方差
s²见下表所示：

甲

乙

丙

丁

$\text{[math]}$

8

9

9

8

s²

1

1

1.2

1.3

从中选一位平均成绩好且成绩稳定的选手参加比赛，应该选（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题
10. 用直尺和圆规作一个直角三角形斜边上的高，作图正确的是（）

A . B . C . D .

查看解析收藏纠错

+选题
11. 在下列命题中，正确的是（）

A . 对角线相等的四边形是平行四边形 B . 有一个角是直角的四边形是矩形 C . 有一组邻边相等的平行四边形是菱形 D . 对角线互相垂直平分的四边形是正方形

查看解析收藏纠错

+选题
12. 如图，将矩形纸片ABCD按如图所示的方式折叠，恰好得到菱形AECF．若AD= $\text{[math]}$ ，则菱形AECF的面积为（）

A . $\text{[math]}$ B . 2 $\text{[math]}$ C . 4 $\text{[math]}$ D . 8

查看解析收藏纠错

+选题

13. 甲、乙、丙三人玩一种游戏，每玩一局都会将三人随机分成两组．积分方法举例说明：第一局甲、乙胜出，分别获得3分，丙获得-6分；第二局甲胜出获得12分，乙、丙分别获得-6分，两局之后的积分是：甲15分，乙3分，丙-12分．下表是三人的逐局积分统计表，计分错误开始于（）

	甲	乙	丙
第一局	3	3	-6
第二局	15	-3	-12
第三局	21	3	-24
第四局	15	-3	-12
第五局	12	-6	-6
第六局	0	18	12

A . 第三局 B . 第四局 C . 第五局 D . 第六局

查看解析收藏纠错

+选题

14. 在如图所示的计算程序中，y与x之间的函数关系所对应的图象应为（）

A . B . C . D .

查看解析收藏纠错

+选题
15. 已知正方形MNKO和正六边形ABCDEF边长均为1，把正方形放在正六边形外边，使OK边与AB边重合，如图所示．按下列步骤操作：
将正方形在正六边形外绕点B顺时针旋转，使KN边与BC边重合，完成第一次旋转；再绕点C顺时针旋转，使NM边与CD边重合，完成第二次旋转；．．．在这样连续6次旋转的过程中，点M在图中直角坐标系中的纵坐标可能是（）

A . 2.2 B . -2.2 C . 2.3 D . -2.3

查看解析收藏纠错

+选题

二、填空题（本大题有3个小题，共12分．17-18小题各3分，19小题6分．）

16. 把二次函数，y=2x²-8x+9，化成y=a(x-h)²+k的形式是：。

查看解析收藏纠错

+选题
17. 用一根长为a(cm)的铁丝，首尾相接围成一个等边三角形。要将它按如图的方式向外等距扩1（cm)，得到新的等边三角形，则新的等边三角形的周长是 cm。

查看解析收藏纠错

+选题
18. 已知A、B两地之间的距离为20千米，甲步行，乙骑车，两人沿着相同路线由A地到B地匀速前行，甲、乙行进的路程S（千米）与x（小时）的函数图象如图所示。

（1）乙比甲晚出发小时；

（2）在整个运动过程中，甲、乙两人之间的距离随x的增大而增大时，x的取值范围是。

查看解析收藏纠错

+选题

三、解答题（本大题共7个小题，共66分，解答应写出文字说明、证明过程或演算步骤）

19. 定义新运算：对于任意数a，b，都有a0b=（a-b）（a²+ab+b²)+b³ ，等式右边是通常的加法、减法、乘法及乘方运算，比如：5⊕2=（5-2）×（5²+5×2+2²)+2³=3×39+8=117+8=125

（1）求3⊕（-2)的值

（2）化简（a-b）(a²+ab+b²)+b³ ．

查看解析收藏纠错

+选题
20. 某学生会倡导的“爱心捐款活动结束后，学生会干部对捐款情况作了抽样调查，并绘制了统计图，图中从左到右各长方形高度之比为3：4：5：8：2，又知此次调查中捐15元和20元的人数共39人。

（1）他们一共抽查了多少人?

（2）这组数据的众数、中位数分别是多少?

（3）若该校共有2310名学生，请估算有多少人捐款数不少于20元？

查看解析收藏纠错

+选题
21. 如图，△MBC和△DBE均为等腰直角三角形．∠ABC=∠DBE=90°
求证：AD=CE；AD⊥CE．

查看解析收藏纠错

+选题
22. 如图，在平面直角坐标系中，□ABCD，顶点A（1，b），B(3，b)，D（2，b+1)

（1）点C的坐标是（用b表示）

（2）双曲线y= $\text{[math]}$ ，过□ABCD的顶点B和D，求该双曲线的表达式

（3）如果□ABCD与双曲线y= $\text{[math]}$ （x>0)总有公共点，求b的取值范围．

查看解析收藏纠错

+选题
23. 发现如图，在有一个“凹角∠A₁A₂A₃”的n边形A₁A₂A₃A₄…A_n中（n为大于3的整数），
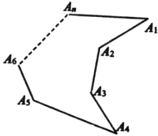
∠A₁A₂A₃=∠A₁+∠A₃+∠A₄+∠A₅+∠A₆+．．．．．+∠A_n-(n-4)×180°

（1）
验证：如图
，
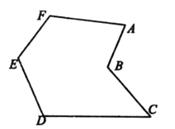
在有一个“凹角∠ABC”的四边形ABCD中，
证明：∠ABC=∠A+∠C+∠D

（2）如图
，
在有一个“凹角∠ABC”的六边形ABCDEF中，
证明：∠ABC=∠A+∠C+∠D+∠E+∠F-360°

（3）
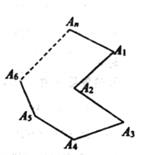
延伸：如图
，
在有两个连续“凹角∠A₁A₂A₃的和∠A₂A₃A₄”的n边形A₁A₂A₃A₄……．．A_n（n为大于4的整数），
∠A₁A₂A₃+∠A₂A₃A₄=∠A₁+∠A₄+∠A₅+∠A₆ ．．．．…+∠A_{n-(n- )}×180

查看解析收藏纠错

+选题
24. 某公司生产的某种时令商品每件成本为20元，经过市场调研发现，这种商品在未来40天内的日销售量m（件）与时间t（天)的关系如下表：

时间t（天）

1

3

5

7

…

日销售量m（件）

94

90

86

82

…

未来40天内，前20天每天的价格y₁（元/件）与时间t（天)的函数关系式为y₁=0.25+25(1≤t≤20，且t为整数），后20天每天的价格y₂=-0.5t+40（21≤t≤40，且t为整数），下面我们来研究销售这种商品的有关问题。

（1）认真分析上表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m（件）与t（天）之间的关系式；

（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？

（3）在实际销售的前20天中，该公司决定每销售一件商品就捐赠a元利润，（a<4)给希望工程．公司通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间t(天)的增大而增大，求a的取值范围．

查看解析收藏纠错

+选题
25. 如图，半圆D的直径AB=4，线段OA=7，O为原点，点B在数轴的正半轴上运动，点B在数轴上所表示的数为m．

（1）当半圆D与数轴相切时，m= ．

（2）半圆D与数轴有两个公共点，设另一个公共点为C．
①直接写出m的取值范围是．

（3）当△A0B的内心、外心与某一个顶点在同一条直线上时，求tan∠AOB的值。

查看解析收藏纠错

+选题

	甲	乙	丙	丁
$\text{[math]}$	8	9	9	8
s²	1	1	1.2	1.3

时间t（天）	1	3	5	7	…
日销售量m（件）	94	90	86	82	…

河北省秦皇岛市暨海港区2018-2019学年中考数学二模考试试卷

一、选择题（本大题共16个小题，共42分．1~10小题各3分，11~16小题各2分．）

二、填空题（本大题有3个小题，共12分．17-18小题各3分，19小题6分．）

三、解答题（本大题共7个小题，共66分，解答应写出文字说明、证明过程或演算步骤）

相关试卷 收起∨

相关试卷收起∨