2012年江苏省南京市中考数学试卷

修改时间：2024-07-12 浏览次数：1060 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 下列四个数中，是负数的是（）

A . |﹣2| B . （﹣2）² C . ﹣ $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为（）

A . 0.25×10^﹣⁵ B . 0.25×10^﹣⁶ C . 2.5×10^﹣⁵ D . 2.5×10^﹣⁶

查看解析收藏纠错

+选题
3. 计算（a²）³÷（a²）²的结果是（）

A . a B . a² C . a³ D . a⁴

查看解析收藏纠错

+选题
4. 12的负的平方根介于（）

A . ﹣5与﹣4之间 B . ﹣4与﹣3之间 C . ﹣3与﹣2之间 D . ﹣2与﹣1之间

查看解析收藏纠错

+选题
5. 若反比例函数 $\text{[math]}$ 与一次函数y=x+2的图象没有交点，则k的值可以是（）

A . ﹣2 B . ﹣1 C . 1 D . 2

查看解析收藏纠错

+选题
6. 如图，在菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在点A′、D′处，且A′D′经过点B，EF为折痕，当D′F⊥CD时， $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

7. 使 $\text{[math]}$ 有意义的x的取值范围是．

查看解析收藏纠错

+选题
8. 计算 $\text{[math]}$ 的结果是．

查看解析收藏纠错

+选题
9. 方程 $\text{[math]}$ ﹣ $\text{[math]}$ =0的解是．

查看解析收藏纠错

+选题
10. 如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角．若∠A=120°，则∠1+∠2+∠3+∠4=

查看解析收藏纠错

+选题
11. 已知一次函数y=kx+k﹣3的图象经过点（2，3），则k的值为

查看解析收藏纠错

+选题
12. 已知下列函数①y=x²；②y=﹣x²；③y=（x﹣1）²+2．其中，图象通过平移可以得到函数y=x²+2x﹣3的图象的有（填写所有正确选项的序号）．

查看解析收藏纠错

+选题
13. 某公司全体员工年薪的具体情况如下表：
年薪
30
14
9
6
4
3.5
3
员工数/人
1
1
1
2
7
6
2
则该公司全体员工年薪的平均数比中位数多万元．

查看解析收藏纠错

+选题
14. 如图，将45°的∠AOB按下面的方式放置在一把刻度尺上：顶点O与尺下沿的端点重合，OA与尺下沿重合，OB与尺上沿的交点B在尺上的读数恰为2cm．若按相同的方式将37°的∠AOC放置在该刻度尺上，则OC与尺上沿的交点C在尺上的读数约为 cm．（结果精确到0.1cm，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看解析收藏纠错

+选题
15. 如图，在▱ABCD中，AD=10cm，CD=6cm，E为AD上一点，且BE=BC，CE=CD，则DE=cm．

查看解析收藏纠错

+选题
16. 在平面直角坐标系中，规定把一个三角形先沿着x轴翻折，再向右平移2个单位称为1次变换．如图，已知等边三角形ABC的顶点B、C的坐标分别是（﹣1，﹣1）、（﹣3，﹣1），把△ABC经过连续9次这样的变换得到△A′B′C′，则点A的对应点A′的坐标是．

查看解析收藏纠错

+选题

三、解答题.

17. 解方程组 $\text{[math]}$ ．

查看解析收藏纠错

+选题
18. 化简代数式 $\text{[math]}$ ，并判断当x满足不等式组 $\text{[math]}$ 时该代数式的符号．

查看解析收藏纠错

+选题
19. 如图，在Rt△ABC中，∠ABC=90°，点D在BC的延长线上，且BD=AB，过点B作BE⊥AC，与BD的垂线DE交于点E．

（1）求证：△ABC≌△BDE；

（2） △BDE可由△ABC旋转得到，利用尺规作出旋转中心O（保留作图痕迹，不写作法）．

查看解析收藏纠错

+选题
20. 某中学七年级学生共450人，其中男生250人，女生200人．该校对七年级所有学生进行了一次体育测试，并随机抽取了50名男生和40名女生的测试成绩作为样本进行分析，绘制成如下的统计表：
成绩
划记
频数
百分比
不及格
9
10%
及格
18
20%
良好
36
40%
优秀
27
30%
合计
90
90
100%

（1）请解释“随机抽取了50名男生和40名女生”的合理性；

（2）从上表的“频数”，“百分比”两列数据中选择一列，用适当的统计图表示；

（3）估计该校七年级体育测试成绩不及格的人数．

查看解析收藏纠错

+选题
21. 甲、乙、丙、丁4名同学进行一次羽毛球单打比赛，要从中选出2名同学打第一场比赛，求下列事件的概率：

（1）已确定甲打第一场，再从其余3名同学中随机选取1名，恰好选中乙同学；

（2）随机选取2名同学，其中有乙同学．

查看解析收藏纠错

+选题
22. 如图，在梯形ABCD中，AD∥BC，AB=DC，对角线AC、BD交于点O，AC⊥BD，E、F、G、H分别是AB、BC、CD、DA的中点．

（1）求证：四边形EFGH是正方形；

（2）若AD=2，BC=4，求四边形EFGH的面积．

查看解析收藏纠错

+选题
23. 看图说故事．
请你编写一个故事，使故事情境中出现的一对变量x、y满足图示的函数关系，要求：

（1）指出变量x和y的含义；

（2）利用图中的数据说明这对变量变化过程的实际意义，其中须涉及“速度”这个量．

查看解析收藏纠错

+选题
24. 某玩具由一个圆形区域和一个扇形区域组成，如图，在⊙O₁和扇形O₂CD中，⊙O₁与O₂C、O₂D分别切于点A、B，已知∠CO₂D=60°，E、F是直线O₁O₂与⊙O₁、扇形O₂CD的两个交点，且EF=24cm，设⊙O₁的半径为xcm．

（1）用含x的代数式表示扇形O₂CD的半径；

（2）若⊙O₁和扇形O₂CD两个区域的制作成本分别为0.45元/cm²和0.06元/cm² ，当⊙O₁的半径为多少时，该玩具的制作成本最小？

查看解析收藏纠错

+选题
25. 某汽车销售公司6月份销售某厂家的汽车，在一定范围内，每部汽车的进价与销售量有如下关系：若当月仅售出1部汽车，则该部汽车的进价为27万元，每多售出1部，所有售出的汽车的进价均降低0.1万元/部，月底厂家根据销售量一次性返利给销售公司，销售量在10部以内（含10部），每部返利0.5万元；销售量在10部以上，每部返利1万元．

（1）若该公司当月售出3部汽车，则每部汽车的进价为万元；

（2）如果汽车的售价为28万元/部，该公司计划当月盈利12万元，那么需要售出多少部汽车？（盈利=销售利润+返利）

查看解析收藏纠错

+选题

26. 下框中是小明对一道题目的解答以及老师的批改．

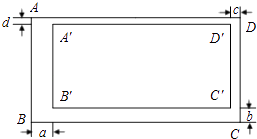
题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1，在温室内，沿前侧内墙保留3m的空地，其他三侧内墙各保留1m的通道，当温室的长与宽各为多少时，矩形蔬菜种植区域的面积是288m²？

解：，

根据题意，得x•2x=288．

解这个方程，得x₁=﹣12（不合题意，舍去），x₂=12

所以温室的长为2×12+3+1=28（m），宽为12+1+1=14（m）

答：当温室的长为28m，宽为14m时，矩形蔬菜种植区域的面积是288m² ．

我的结果也正确！

（1）小明发现他解答的结果是正确的，但是老师却在他的解答中画了一条横线，并打了一个？．结果为何正确呢？

（2）请指出小明解答中存在的问题，并补充缺少的过程：

变化一下会怎样…

（3）如图，矩形A′B′C′D′在矩形ABCD的内部，AB∥A′B′，AD∥A′D′，且AD：AB=2：1，设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d，要使矩形A′B′C′D′∽矩形ABCD，a、b、c、d应满足什么条件？请说明理由．

查看解析收藏纠错

+选题

27. 如图，A、B是⊙O上的两个定点，P是⊙O上的动点（P不与A、B重合）、我们称∠APB是⊙O上关于点A、B的滑动角．

（1）已知∠APB是⊙O上关于点A、B的滑动角，
①若AB是⊙O的直径，则∠APB=°；②若⊙O的半径是1，AB= $\text{[math]}$ ，求∠APB的度数；

（2）已知O₂是⊙O₁外一点，以O₂为圆心作一个圆与⊙O₁相交于A、B两点，∠APB是⊙O₁上关于点A、B的滑动角，直线PA、PB分别交⊙O₂于M、N（点M与点A、点N与点B均不重合），连接AN，试探索∠APB与∠MAN、∠ANB之间的数量关系．

查看解析收藏纠错

+选题

成绩	划记	频数	百分比
不及格		9	10%
及格		18	20%
良好		36	40%
优秀		27	30%
合计	90	90	100%

年薪	30	14	9	6	4	3.5	3
员工数/人	1	1	1	2	7	6	2

2012年江苏省南京市中考数学试卷

一、选择题

二、填空题

三、解答题.

相关试卷 收起∨

相关试卷收起∨