修改时间:2024-07-12 浏览次数:617 类型:中考真卷
数学课上,李老师出示了如下框中的题目.

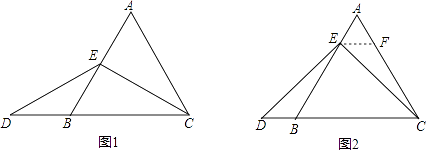
小敏与同桌小聪讨论后,进行了如下解答:
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AEDB(填“>”,“<”或“=”).
解:题目中,AE与DB的大小关系是:AEDB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
试题篮