2017年山东省潍坊市安丘市中考数学模拟试卷

修改时间：2024-07-12 浏览次数：1377 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. （ $\text{[math]}$ ）的倒数是（）

A . $\text{[math]}$ B . 8 C . ﹣8 D . ﹣1

查看解析收藏纠错

+选题
2. 如图，是某几何体的三视图及相关数据，则该几何体的侧面积是（）

A . 10π B . 15π C . 20π D . 30π

查看解析收藏纠错

+选题
3. 下列运算正确的是（）

A . 4a²﹣4a²=4a B . （﹣a³b）²=a⁶b² C . a+a=a² D . a²•4a⁴=4a⁸

查看解析收藏纠错

+选题
4. 如图，EF∥BC，AC平分∠BAF，∠B=80°，∠C=（）度．

A . 40 B . 45 C . 50 D . 55

查看解析收藏纠错

+选题
5. 下列运算正确的是（）

A . x³•x⁵=x¹⁵ B . （x²）⁵=x⁷ C . $\text{[math]}$ =3 D . $\text{[math]}$ =﹣1

查看解析收藏纠错

+选题
6. 三角形的两边长分别为3和6，第三边的长是方程x²﹣6x+8=0的一个根，则这个三角形的周长是（）

A . 9 B . 11 C . 13 D . 11或13

查看解析收藏纠错

+选题
7. 若关于x的一元一次不等式组 $\text{[math]}$ 有解，则m的取值范围为（）

A . $\text{[math]}$ B . m≤ $\text{[math]}$ C . m＞ $\text{[math]}$ D . m≤ $\text{[math]}$

查看解析收藏纠错

+选题
8. 把直线y=﹣x+3向上平移m个单位后，与直线y=2x+4的交点在第一象限，则m的取值范围是（）

A . 1＜m＜7 B . 3＜m＜4 C . m＞1 D . m＜4

查看解析收藏纠错

+选题
9. 估计 $\text{[math]}$ 介于之间．（）

A . 1.4与1.5 B . 1.5与1.6 C . 1.6与1.7 D . 1.7与1.8

查看解析收藏纠错

+选题
10. 如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（）

A . AB=BE B . BE⊥DC C . ∠ADB=90° D . CE⊥DE

查看解析收藏纠错

+选题
11. 要制作一个圆锥形的烟囱帽，使底面圆的半径与母线长的比是4：5，那么所需扇形铁皮的圆心角应为（）

A . 288° B . 144° C . 216° D . 120°

查看解析收藏纠错

+选题
12. 已知二次函数y=ax²+bx+1（a＜0）的图象过点（1，0）和（x₁ ， 0），且﹣2＜x₁＜﹣1，下列5个判断中：①b＜0；②b﹣a＜0；③a＞b﹣1；④a＜﹣ $\text{[math]}$ ；⑤2a＜b+ $\text{[math]}$ ，正确的是（）

A . ①③ B . ①②③ C . ①②③⑤ D . ①③④⑤

查看解析收藏纠错

+选题

二、填空题

13. 如图：△ABC中，AB=AC，内切圆⊙O与边BC、AB分别切于点D、E、F，若∠C=30°，CE=2 $\text{[math]}$ ，则AC=．

查看解析收藏纠错

+选题
14. 因式分解：﹣2x²y+12xy﹣16y=．

查看解析收藏纠错

+选题
15. 已知 $\text{[math]}$ 是二元一次方程组 $\text{[math]}$ 的解，则m+3n的立方根为．

查看解析收藏纠错

+选题
16. 如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为．

查看解析收藏纠错

+选题
17. 如图，在平面直角坐标系xOy中，四边形ODEF和四边形ABCD都是正方形，点F在x轴的正半轴上，点C在边DE上，反比例函数y= $\text{[math]}$ （k≠0，x＞0）的图象过点B，E．若AB=2，则k的值为．

查看解析收藏纠错

+选题
18.
如图四边形ABCD中，AD=DC，∠DAB=∠ACB=90°，过点D作DF⊥AC，垂足为F．DF与AB相交于E．设AB=15，BC=9，P是射线DF上的动点．当△BCP的周长最小时，DP的长为．

查看解析收藏纠错

+选题

三、解答题

19. 计算下列各题

（1）计算：（ $\text{[math]}$ ）^﹣²﹣6sin30°﹣（ $\text{[math]}$ ）⁰+ $\text{[math]}$ +| $\text{[math]}$ ﹣ $\text{[math]}$ |

（2）化简：（ $\text{[math]}$ ﹣ $\text{[math]}$ ）÷ $\text{[math]}$ ，然后请自选一个你喜欢的x值，再求原式的值．

查看解析收藏纠错

+选题
20. 今年我市某公司分两次采购了一批大蒜，第一次花费40万元，第二次花费60万元．已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元，第二次采购时每吨大蒜的价格比去年的平均价格下降了500元，第二次的采购数量是第一次采购数量的两倍．

（1）试问去年每吨大蒜的平均价格是多少元？

（2）该公司可将大蒜加工成蒜粉或蒜片，若单独加工成蒜粉，每天可加工8吨大蒜，每吨大蒜获利1000元；若单独加工成蒜片，每天可加工12吨大蒜，每吨大蒜获利600元．由于出口需要，所有采购的大蒜必需在30天内加工完毕，且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半，为获得最大利润，应将多少吨大蒜加工成蒜粉？最大利润为多少？

查看解析收藏纠错

+选题
21.
如图，一枚运载火箭从地面O处发射，当火箭到达A点时，从地面C处的雷达站测得AC的距离是6km，仰角是43°，1s后，火箭到达B点，此时测得仰角为45.5°，这枚火箭从点A到点B的平均速度是多少？（结果精确到0.01）

查看解析收藏纠错

+选题
22. 我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元．
经市场调研发现：该款工艺品每天的销售量y（件）与售价x（元）之间存在着如下表所示的一次函数关系．
售价x（元）
…
70
90
…
销售量y（件）
…
3000
1000
…
（利润=（售价﹣成本价）×销售量）

（1）求销售量y（件）与售价x（元）之间的函数关系式；

（2）你认为如何定价才能使工艺品厂每天获得的利润为40000元？

查看解析收藏纠错

+选题
23.
将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，如图①所示，∠BAB′=θ， $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ =n，我们将这种变换记为[θ，n]．

（1）
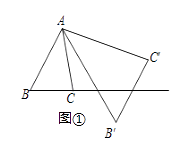
如图①，对△ABC作变换[60°， $\text{[math]}$ ]得到△AB′C′，则S_△_AB'C：S_△_ABC=；直线BC与直线B′C′所夹的锐角为度；

（2）
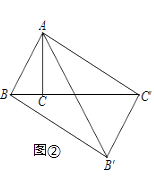
如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、C′在同一直线上，且四边形ABB′C′为矩形，求θ和n的值；

（3）
如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．

查看解析收藏纠错

+选题

售价x（元）	…	70	90	…
销售量y（件）	…	3000	1000	…

2017年山东省潍坊市安丘市中考数学模拟试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨