2016-2017学年江西省景德镇市九年级上学期期中数学试卷

修改时间：2024-07-12 浏览次数：642 类型：期中考试编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 将一元二次方程3x²+1=6x化为一般形式后，常数项为1，则一次项系数为（）

A . 3 B . ﹣6 C . ﹣3 D . 6

查看解析收藏纠错

+选题
2. 在矩形ABCD中，AC与BD相交于点O，若∠DBC=34°，则∠AOB等于（）

A . 34° B . 56° C . 68° D . 73°

查看解析收藏纠错

+选题
3. 用配方法解方程x²+4x+1=0，配方后的方程是（）

A . （x+2）²=5 B . （x﹣2）²=3 C . （x﹣2）²=5 D . （x+2）²=3

查看解析收藏纠错

+选题
4.
如图，已知直线a∥b∥c ，直线m、n与直线a、b、c分别交于点A、C、E、B、D、F ， AC=4，CE=6，BD=3，则BF=（　　）.

A . 7 B . 7.5 C . 8 D . 8.5

查看解析收藏纠错

+选题
5. 如图所示平面内，有一靠在墙面上的梯子AB（粗细忽略不计），因外界因素导致梯子底端A持续向右滑动，直至整架梯子完全滑落到地面（即B与O重合），设A向右滑动的距离为x（cm），梯子的中点M与墙角O之间的距离为y（cm），则在整个滑动过程中，y与x的关系大致可表达为下列图象中的（）

A . B . C . D .

查看解析收藏纠错

+选题
6. 一张等腰三角形纸片，底边长15cm，底边上的高长22.5cm，现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条（如图所示），则裁得的纸条中恰为张正方形的纸条是（）

A . 第4张 B . 第5张 C . 第6张 D . 第7张

查看解析收藏纠错

+选题

二、填空题

7. 若方程（m﹣1）x²﹣4x+3=0是一元二次方程，当m满足条件．

查看解析收藏纠错

+选题
8. 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题
9. 近年来我市大力发展旅游产业，旅游总收入从2013年的150亿元上升到2015年的200亿元，设这两年旅游总收入的年平均增长率为x，则可列方程．

查看解析收藏纠错

+选题
10. 如图，▱ABCD中，对角线AC，BD相交于点O，且AC⊥BD，请你添加一个适当的条件，使ABCD成为正方形．

查看解析收藏纠错

+选题
11. 若（x²+y²）（1﹣x²﹣y²）+6=0，则x²+y²的值是．

查看解析收藏纠错

+选题
12. 如图，在△ABC中∠ABC=90°，∠A=30°，BC=2cm，动点P以3cm/s的速度由A沿射线AC方向运动，动点Q同时以1cm/s的速度由B向CB的延长线方向运动，连PQ交直线AB于D，则当运动时间为s时，△ADP是等腰三角形．

查看解析收藏纠错

+选题

三、解答题

13. 综合题。

（1）解方程：x²=2x．

（2）如图，Rt△ABC中，∠BAC=90°，AB=5，AC=12，将△ABC向右平移至△A′B′C′的位置，使得四边形ABB′A′为菱形，求B′C的长．

查看解析收藏纠错

+选题
14. 已知关于x的方程x²+x+a﹣1=0有一个根是1，求a的值及方程的另一个根．

查看解析收藏纠错

+选题
15. 如图，在△ABC中，∠C=90°，点E，F分别在边AB，BC上，沿直线EF将△EBF翻折，使顶点B的对应点B₁落在AC边上，且EB₁⊥AC．求证：四边形BFB₁E是菱形．

查看解析收藏纠错

+选题
16. 小明的手机没电了，现有一个只含A，B，C，D四个同型号插座的插线板（如图，假设每个插座都适合所有的充电插头，且被选中的可能性相同），请计算：

（1）若小明随机选择一个插座插入，则插入A的概率为；

（2）现小明对手机和学习机两种电器充电，请用列表或画树状图的方法表示出两个插头插入插座的所有可能情况，并计算两个插头插在相邻插座的概率．

查看解析收藏纠错

+选题
17. 在正方形ABCD中，点P是BC的中点，仅用无刻度的直尺按要求画图：

（1）在图①中画出AD的中点M；

（2）在图②中画出对角线AC的三等分点E，点F．

查看解析收藏纠错

+选题
18. 已知关于x的方程x²﹣2（k﹣1）x+k²=0，

（1）当k为何值时，方程有实数根；

（2）设x₁ ， x₂是方程的两个实数根，且x₁²+x₂²=4，求k的值．

查看解析收藏纠错

+选题
19. 如图所示，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为1：3，点A，B，E在x轴上．

（1）若点F的坐标为（6，3），直接写出点C和点A的坐标；

（2）若正方形BEFG的边长为6，求点C的坐标．

查看解析收藏纠错

+选题
20. 我市某社会团体组织人员参观皇窑瓷展，主办方对团体购票实行优惠：在原定票价的基础上，每张降价40元，则按原定票价需花费6000元购买门票，现在只花了4000元．

（1）求每张门票原定的票价；

（2）在展览期间，平均每天可售出个人票2000张，现主办方决定对个人购票也采取优惠措施，发现原定票价每降低2元，平均每天可多售出个人票40张，若要使平均每天的个人票收入达到241500元，且能有效控制游览人数，则票价应降低多少元？

查看解析收藏纠错

+选题
21. 如果，矩形ABCD中，点E在AB上，点F在CD上，点G，H在对角线AC上，且CH=AG，CF=AE．

（1）求证：△AGE≌△CHF；

（2）若AB=8，AD=4，且GH恰好平分∠FGE，求CF的长．

查看解析收藏纠错

+选题
22.
如图，在平面直角坐标系中，已知Rt△AOB的两直角边OA，OB分别在x轴，y轴的正半轴上（OA＜OB），且OA，OB的长分别是一元二次方程x²﹣14x+48=0的两个根，线段AB的垂直平分线CD交AB于点C，分别交x轴，y轴于点D，E．

（1）直接写出点A、B的坐标：A，B；

（2）求线段AD的长；

（3）已知P是直线CD上一个动点，点Q是直线AB上一个动点，则在坐标平面内是否存在点M，使得以点C、P、Q、M为顶点的四边形是以5为边长的正方形？若存在，直接写出点M的坐标；若不存在，说明理由．

查看解析收藏纠错

+选题
23. 【定义】已知P为△ABC所在平面内一点，连接PA，PB，PC，在△PAB，△PBC和△PAC中，若存在一个三角形与△ABC相似（全等除外），那么就称P为△ABC的“共相似点”，根据“共相似点”是否落在三角形的内部，边上或外部，可将其分为“内共相似点”，“边共相似点”或“外共相似点”．

（1）据定义可知，等边三角形（填“存在”或“不存在”）共相似点．

（2）
如图1，若△ABC的一个边共相似点P与其对角顶点B的连线，将△ABC分割成的两个三角形恰与原三角形均相似，试判断△ABC的形状，并说明理由．

（3）
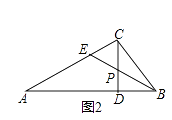
如图2，在△ABC中，∠A＜∠B＜∠C，高线CD与角平分线BE交于点P，若P是△ABC的一个内共相似点，试说明点E是△ABC的边共相似点，并直接写出∠A的度数．

（4）
如图3，在Rt△ABC中，∠C=90°，∠A=30°，BC= $\text{[math]}$ ，若△PBC与△ABC相似，则满足条件的P点共有个，顺次连接所有满足条件的P点而围成的多边形的周长为．

查看解析收藏纠错

+选题

2016-2017学年江西省景德镇市九年级上学期期中数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨