江苏省盐城市南洋中学2018-2019学年八年级上学期数学期中考试试卷

1. 下面四个图形分别是低碳、节水、节能和绿色食品标志，在这四个标志中，是轴对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
2. 下列长度的三条线段能组成直角三角形的是（）

A . 3，4，5 B . 2，3，4 C . 4，6，7 D . 5，11，12

查看解析收藏纠错

+选题
3. 如图，△ACB≌△A′CB′，∠B=50°，则∠B′的度数为（）

A . 20° B . 30° C . 35° D . 50°

查看解析收藏纠错

+选题
4. 如图，OC是∠AOB的平分线，PD⊥DA于点D，PD=2，则P点到OB的距离是（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
5. 如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的（）

A . CB=CD B . ∠ BAC=∠DAC C . ∠BCA=∠DCA D . ∠B=∠D=90⁰

查看解析收藏纠错

+选题
6. 到三角形三个顶点的距离相等的点是（）

A . 三条角平分线的交点 B . 三边中线的交点 C . 三边上高所在直线的交点 D . 三边的垂直平分线的交点

查看解析收藏纠错

+选题
7. 如图，在Rt△ABC中，∠B=90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知∠BAE=10°，则∠C的度数为（）

A . 30° B . 40° C . 50° D . 60°

查看解析收藏纠错

+选题
8. 如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为（）

A . 90° B . 60° C . 45° D . 30°

查看解析收藏纠错

+选题

9. 已知等腰三角形的两条边长分别为2和5，则它的周长为．

查看解析收藏纠错

+选题
10. 在Rt△ABC中，斜边上的中线长为5cm，则斜边长为．

查看解析收藏纠错

+选题
11. 一个等腰三角形的一个角为80°，则它的顶角的度数是．

查看解析收藏纠错

+选题
12. 一个直角三角形的两直角边长分别为5cm和12cm,则斜边长为cm.

查看解析收藏纠错

+选题
13. 如图是某天下午小明在镜中看到身后墙上的时钟情况，则实际时间大约是．

查看解析收藏纠错

+选题
14. 如图，△ABC中，∠BAC=90°，BC=6，以△ABC的三边向外作正方形，以AC为边的正方形的面积为25cm² ，则正方形M的面积为cm² ．

查看解析收藏纠错

+选题
15. 如图，在△ABC中，点D是BC上一点，∠BAD=80°，AB=AD=DC，则∠C=°.

查看解析收藏纠错

+选题
16. 如图，已知在△ABC中，DE是BC的垂直平分线，垂足为E，交AC于点D，若AB=6，AC=9，则△ABD的周长是．

查看解析收藏纠错

+选题
17. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连结AA′，若∠AA′B′=20°，则∠B的度数为°．

查看解析收藏纠错

+选题
18. 如图，在△ABC中，∠ACB=90°，∠BAC=30°，在直线BC或AC上取一点P，使得△PAB为等腰三角形，这样的点P共有个.

查看解析收藏纠错

+选题

19. 在下列的图形上补一个小正方形，使它成为一个轴对称图形，并画出对称轴．

查看解析收藏纠错

+选题
20. 如图，在正方形网格中，每个小正方形的边长都是1，每个小正方形的顶点叫做格点．网格中有一个格点△ABC（即三角形的顶点都在格点上）．

（1）在图中作出△ABC关于直线l对称的△A₁B₁C₁（要求A与A₁ ， B与B₁ ， C与C₁相对应）；

（2）求△ABC的面积；

（3）在直线l上找一点P，使得△PAC的周长最小．

查看解析收藏纠错

+选题
21. 如图，点A、D、B、E在一条直线上，AD=BE，∠C=∠F，BC∥EF.求证：

（1） △ABC≌DEF

（2） AC∥DF

查看解析收藏纠错

+选题
22. 如图，花果山上有两只猴子在一棵树CD上的点B处，且BC=5m，它们都要到A处吃东西，其中一只猴子甲沿树爬下走到离树10m处的池塘A处，另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处．已知两只猴子所经过的路程相等，设BD为xm．

（1）请用含有x的整式表示线段AD的长为m；

（2）求这棵树高有多少米？

查看解析收藏纠错

+选题
23. 已知：如图∠ABC=∠ADC=90°，M，N分别是AC、BD的中点．求证：MN⊥BD．

查看解析收藏纠错

+选题
24. 如图，△ACB和△ECD都是等边三角形，点A、D、E在同一直线上，连接BE．

（1）求证：AD=BE；

（2）求∠AEB的度数．

查看解析收藏纠错

+选题
25. 定义：如图，点M、N把线段AB分割成AM、MN、NB，若以AM、MN、NB为边的三角形是一个直角三角形，则称点M、N是线段AB的勾股分割点．

（1）已知M、N把线段AB分割成AM、MN、NB，若AM=1.5，MN=2.5，BN=2，则点M、N是线段AB的勾股分割点吗？请说明理由．

（2）已知点M、N是线段AB的勾股分割点，且AM为直角边，若AB=24，AM=6，求BN的长．

查看解析收藏纠错

+选题
26.

（1）【问题情境】
课外兴趣小组活动时，老师提出了如下问题：

如图①，△ABC中，若AB＝10，AC＝8，求BC边上的中线AD的取值范围．

小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE＝AD，连接BE．请根据小明的方法思考：

Ⅰ.由已知和作图能得到△ADC≌△EDB，依据是．

A．SSS B．SAS C．AAS D．HL

Ⅱ.由“三角形的三边关系”可求得AD的取值范围是．

（2）【解后反思】题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．
【初步运用】如图②，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF．若EF＝4，EC＝3，求线段BF的长．

（3）【灵活运用】
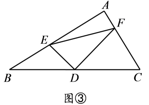
如图③，在△ABC中，∠A＝90°，D为BC中点， DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．试猜想线段BE、CF、EF三者之间的等量关系，并证明你的结论．

查看解析收藏纠错

+选题

江苏省盐城市南洋中学2018-2019学年八年级上学期数学期中考试试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

江苏省盐城市南洋中学2018-2019学年八年级上学期数学期中考试试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨