【提升卷】2024年北师大版数学八（下）6.3三角形的中位线同步练习

1. 如图，M 是△ABC的边 BC 的中点，AN平分∠BAC，BN⊥AN，且 AB=10，MN=3，则AC的长（）

A . 12 B . 14 C . 16 D . 18

查看解析收藏纠错

+选题
2. 如图，□ABCD的周长为 36，对角线 AC，BD 相交于点O，E 是CD 的中点，连结OE.若 BD =12，则△DOE 的周长为（）

A . 15 B . 18 C . 21 D . 24

查看解析收藏纠错

+选题
3. 如图，在△ABC中，∠C=90°，E是CA延长线上-点，F是CB上一点，AE=12，BF=8，点P，Q，D分别是AF ，BE，AB的中点，则PQ的长为（）

A . $\text{[math]}$ B . 4 C . 6 D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图， $\text{[math]}$ ABCD的对角线AC，BD相交于点O，∠ADC的平分线与边AB相交于点P，E是PD中点，若AD=4，CD=6，则EO的长为（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
5. 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ ， $\text{[math]}$ 上的动点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值与最小值的差为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，点D，E分别是 $\text{[math]}$ 的边 $\text{[math]}$ 上的中点， $\text{[math]}$ 的角平分线交 $\text{[math]}$ 于点F， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 1 B . 1.5 C . 2 D . 2.5

查看解析收藏纠错

+选题
7. 如图，△ABC的中线BD、CE交于点O，连接OA，点G，F分别为OC，OB的中点，BC=4，AO=3，则四边形DEFG的周长为（）

A . 6 B . 7 C . 8 D . 12

查看解析收藏纠错

+选题
8. 如图，直线y= $\text{[math]}$ x+4与x轴、y轴分别交于点A和点B，点C，D分别为线段AB，OB的中点，点P为OA边上的一个动点，当PC+PD值最小时，点P的坐标为（）

A . $\text{[math]}$ B . (-6，0) C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

9. 如图，EF是△ABC的中位线，BD平分∠ABC交EF于点D ，若AE＝3，DF＝1，则边BC的长为．

查看解析收藏纠错

+选题
10. 如图，四边形ABCD中，∠A＝90°，AB＝2 $\text{[math]}$ ，AD＝2，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为．

查看解析收藏纠错

+选题
11. 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上的中点， $\text{[math]}$ 为 $\text{[math]}$ 边上一点， $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 延长线于 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
12. 如图，D，E分别是△ABC的边AB，AC的中点，连结DE，BE，过点C作CF∥BE，交 DE的延长线于点F.若EF=3，则DE的长为.

查看解析收藏纠错

+选题
13. 如图，△ABC的周长为 28，点 D，E都在边BC 上，∠ABC 的平分线垂直于 AE，垂足为 Q，∠ACB的平分线垂直于 AD，垂足为 P，连结PQ.若 BC=10，则PQ的长是.

查看解析收藏纠错

+选题

14. 如图，在四边形ABCD中，AC＝BD ， AC、BD交于点O ， E、F分别是AB、CD中点，EF分别交AC、BD于点H、G ．求证：OG＝OH ．

查看解析收藏纠错

+选题
15. 在 $\text{[math]}$ 中， $\text{[math]}$ ， E、F分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，延长 $\text{[math]}$ 到点D，使 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点O．

（1）试说明 $\text{[math]}$ 与 $\text{[math]}$ 互相平分；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
16. 如图，在平行四边形 $\text{[math]}$ 中，E，F分别是 $\text{[math]}$ ， $\text{[math]}$ 边上的点， $\text{[math]}$ ，连接 $\text{[math]}$ 和 $\text{[math]}$ 的交点为M， $\text{[math]}$ 和 $\text{[math]}$ 的交点为N，连接 $\text{[math]}$ ， $\text{[math]}$ ．

（1）求证：四边形 $\text{[math]}$ 为平行四边形．

（2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
17. 阅读与思考
请阅读下列材料，并完成相应的任务．
$\text{[math]}$ 年 $\text{[math]}$ 月 $\text{[math]}$ 日星期一
今天，同学们学习了三角形中位线定理的相关内容，知道了“三角形的中位线平行于第三边，且等于第三边的一半”．课下，对三角形中位线定理的相关知识进行了复习，并对它相关的命题产生了兴趣．如图1，在 $\text{[math]}$ 中， $\text{[math]}$ 分别是 $\text{[math]}$ 边上的点，同学们提出了以下三个命题：

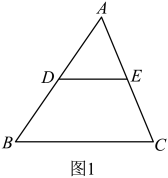
I.若 $\text{[math]}$ 是 $\text{[math]}$ 边的中点，且 $\text{[math]}$ ，则 $\text{[math]}$ 是 $\text{[math]}$ 边的中点．
II.若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 分别是 $\text{[math]}$ 边的中点．
III.若 $\text{[math]}$ 是 $\text{[math]}$ 边的中点，且 $\text{[math]}$ ，则 $\text{[math]}$ 是 $\text{[math]}$ 边的中点．
任务：

（1）从所提出的三个命题中选择一个假命题，并在图2中画出反例．（要求：尺规作图，保留作图痕迹）

（2）从所提出的三个命题中选择一个真命题进行证明．

查看解析收藏纠错

+选题

【提升卷】2024年北师大版数学八（下）6.3三角形的中位线同步练习

一、选择题

二、填空题

三、综合题

相关试卷收起∨

【提升卷】2024年北师大版数学八（下）6.3三角形的中位线 同步练习

一、选择题

二、填空题

三、综合题

相关试卷 收起∨

【提升卷】2024年北师大版数学八（下）6.3三角形的中位线同步练习

相关试卷收起∨