2023-2024学年湘教版初中数学七年级下册 2.1.4 多项式的乘法同步分层训练培优题

1. 要使多项式 $\text{[math]}$ 不含x的一次项，则m的值为（）

A . 0 B . 1 C . 2 D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 若 $\text{[math]}$ 的积中不含 $\text{[math]}$ 的一次项，那么 $\text{[math]}$ 与 $\text{[math]}$ 一定是（）

A . 互为相反数 B . 互为倒数 C . 相等 D . $\text{[math]}$ 比 $\text{[math]}$ 大

查看解析收藏纠错

+选题
3. 已知(x+a)(x+b)=x²+mx+24，其中a，b为整数，则整数m可能的取值有（）个.

A . 2 B . 4 C . 6 D . 8

查看解析收藏纠错

+选题
4. 如图1，有边长分别为a和b（a>b）的A类和B类正方形纸片、长为a、宽为b的C类矩形纸片若干张，要拼一个边长为a+b的正方形（如图2所示），则需要1张A类纸片、1张B类纸片和⒉张C类纸片.若要拼一个长为3a+b、宽为2a+2b的矩形，则需要C类纸片的张数为（）

A . 6 B . 7 C . 8 D . 9

查看解析收藏纠错

+选题
5. (x-a)(x²+ax+a²)的计算结果是（）

A . x³+2ax+a³ B . x³-a³ C . x³+2a²x+a³ D . x²+2ax²+a³

查看解析收藏纠错

+选题
6. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 $\text{[math]}$ 为非负整数）的展开式中，把各项系数按一定的规律排成右表（展开后每一项按 $\text{[math]}$ 的次数由大到小的顺序排列）．人们把这个表叫做“杨辉三角”．据此规律，则 $\text{[math]}$ 展开式中含 $\text{[math]}$ 项的系数是 $\text{[math]}$ 　　 $\text{[math]}$

A . 2016 B . 2017 C . 2018 D . 2019

查看解析收藏纠错

+选题
7. 如图1的8张宽为a，长为 $\text{[math]}$ 的小长方形纸片，按如图2的方式不重叠地放在长方形ABCD内，未被覆盖的部分（两个长方形）用阴影表示.设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，在我国南宋数学家杨辉所著的《详解九章算术》一书中，介绍了(a+b)ⁿ展开式的系数规律，称为“杨辉三角”．如第5行的5个数是1，4，6，4，1，恰好对应着 $\text{[math]}$ 展开式中的各项系数．利用上述规律计算关于x的多项式 $\text{[math]}$ 中 $\text{[math]}$ 项的系数为（）

A . 80 B . 60 C . 40 D . 20

查看解析收藏纠错

+选题

9. 若 $\text{[math]}$ ．则m＝．

查看解析收藏纠错

+选题
10. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图一）就是一例．这个三角形给出了（a+b）ⁿ（n＝1，2，3，4，5，6…）的展开式的系数规律．请你仔细观察下表中的规律，按照上述规律，则（a+b）⁶展开式中第二项的系数是；（a+b）⁹⁸展开式中第三项的系数是．

查看解析收藏纠错

+选题
11. 已知 $\text{[math]}$ 的展开式中不含 $\text{[math]}$ 和 $\text{[math]}$ 项，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
12. 如图，正方形卡片A类、B类和长方形卡片C类各若干张（a≠b），如果要选用上述3类卡片共12张拼成一个大长方形（拼接时不可重叠，不可有缝隙）、且卡片全部用上，则不同的选取方案有种．

查看解析收藏纠错

+选题
13. 用纸片拼图时，我们发现利用图1中的三种纸片（边长分别为 $\text{[math]}$ ， $\text{[math]}$ 的正方形和长为 $\text{[math]}$ 宽为 $\text{[math]}$ 的长方形）各若干，可以拼出一些长方形来解释某些等式，比如图2可以解释为： $\text{[math]}$ ．

（1）图3可以解释为等式：；

（2）要拼出一个两边长为 $\text{[math]}$ ， $\text{[math]}$ 的长方形，先回答需要以下三种纸片各多少块，再用画图或整式乘法验证你的结论；
块，块，块

（3）如图4，大正方形的边长为 $\text{[math]}$ ，小正方形的边长为 $\text{[math]}$ ，若用 $\text{[math]}$ ， $\text{[math]}$ （ $\text{[math]}$ ）表示四个相同小长方形的两边长，以下关系式正确的是（填序号）．① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ．

查看解析收藏纠错

+选题

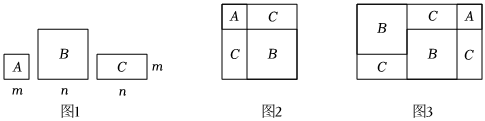
14. 教材中，在计算如图1所示的正方形ABCD的面积时，分别从两个不同的角度进行了操作：

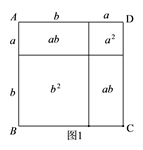
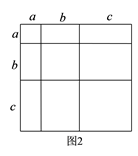
（1）把它看成是一个大正方形，则它的面积为 $\text{[math]}$ ；
（2）把它看成是2个小长方形和2个小正方形组成的，则它的面积为 $\text{[math]}$ ；因此，可得到等式： $\text{[math]}$ .
① 类比教材中的方法，由图2中的大正方形可得等式：                          .
② 试在图2右边空白处画出面积为 $\text{[math]}$ 的长方形的示意图（标注好a、b），由图形可知，多项式 $\text{[math]}$ 可分解因式为：                          ．
在上方空白处画出②中的示意图
③ 若将代数式 $\text{[math]}$ 展开后合并同类项，得到多项式N，则多项式N的项数一共有                          项.

查看解析收藏纠错

+选题
15. 数形结合是解决数学问题的重要思想方法，借助图形可以对很多数学问题进行直观推导和解释 $\text{[math]}$ 如图 $\text{[math]}$ ，有足够多的 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种纸片： $\text{[math]}$ 种是边长为 $\text{[math]}$ 的正方形， $\text{[math]}$ 种是边长为 $\text{[math]}$ 的正方形， $\text{[math]}$ 种是宽为 $\text{[math]}$ ，长为 $\text{[math]}$ 的长方形 $\text{[math]}$ 用 $\text{[math]}$ 种纸片 $\text{[math]}$ 张， $\text{[math]}$ 种纸片 $\text{[math]}$ 张， $\text{[math]}$ 种纸片 $\text{[math]}$ 张可以拼出 $\text{[math]}$ 不重不漏 $\text{[math]}$ 如图 $\text{[math]}$ 所示的正方形 $\text{[math]}$ 根据正方形的面积，可以用来解释整式乘法 $\text{[math]}$ ，反过来也可以解释多项式 $\text{[math]}$ ，因式分解的结果为 $\text{[math]}$ ，依据上述积累的数与形对应关系的经验，解答下列问题：

（1）若多项式 $\text{[math]}$ 表示分别由 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 张 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种纸片拼出如图 $\text{[math]}$ 所示的大长方形的面积，请根据图形求出这个长方形的长和宽，并对多项式 $\text{[math]}$ 进行因式分解；

（2）我们可以借助图 $\text{[math]}$ 再拼出一个更大的长方形，使该长方形刚好由 $\text{[math]}$ 张 $\text{[math]}$ 种纸片， $\text{[math]}$ 张 $\text{[math]}$ 种纸片， $\text{[math]}$ 张 $\text{[math]}$ 种纸片拼成，那么这个长方形的面积可以表示为多项式，据此可得到该多项式因式分解的结果为．

查看解析收藏纠错

+选题

16.

（1）计算观察下列各式填空：
第1个： $\text{[math]}$ ；
第2个： $\text{[math]}$ ；
第3个： $\text{[math]}$ ；
这些等式反映出多项式乘法的某种运算规律．

（2）猜想：若n为大于1的正整数，则 $\text{[math]}$ ．

（3）利用（2）的猜想结论计算： $\text{[math]}$ ．

（4）扩展与应用： $\text{[math]}$ ．

查看解析收藏纠错

+选题
17. 18世纪欧拉引进了求和符号“ $\text{[math]}$ ”（其中 $\text{[math]}$ ，且i和n表示正整数），对这个符号我们进行如下定义： $\text{[math]}$ 表示k从i开始取数一直取到n，全部加起来，即 $\text{[math]}$ ．例如：当i=1时， $\text{[math]}$ ．

（1） ① $\text{[math]}$ ， ② $\text{[math]}$ ， ③ $\text{[math]}$ 中和为45的是；（填写编号）

（2） $\text{[math]}$ ；

（3） $\text{[math]}$ ；（用含n的式子表示）

（4）若 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

查看解析收藏纠错

+选题

2023-2024学年湘教版初中数学七年级下册 2.1.4 多项式的乘法同步分层训练培优题

一、选择题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

2023-2024学年湘教版初中数学七年级下册 2.1.4 多项式的乘法同步分层训练培优题

一、选择题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨