备考浙教版中考数学题型专项训练统计与概率解答题专练

修改时间：2022-05-23 浏览次数：80 类型：三轮冲刺编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、综合题

1. 2021年12月，中共玉溪市红塔区委办公室、玉溪市红塔区人民政府办公室印发《玉溪市红塔区进一步减轻义务教育阶段学生作业负担和校外培训负担的实施方案》，文件明确要求，建立作业统筹管理机制，科学合理布置作业，严控作业总量和时长，切实减轻学生过重课业负担，初中学生每天书面作业平均完成时间不超过90分钟，周末、寒暑假、法定节假日也控制书面作业时间，某校为了解在“双减”政策下九年级学生每天书面作业完成时间（单位：分钟）的落实情况，在九年级学生中随机抽取部分学生进行了一次问卷调查，并将调查结果统计如下表：
每天书面完成时间t/分钟
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
人数
2
10
15
17
6

（1）直接写出本次调查的样本容量，中位数所在的范围及平均数（计算平均数时，可用各组的组中值代表各组的实际数据）；

（2）直接写出抽取的学生每天书面作业完成时间超过90分钟的人数，估计该校九年级学生每天书面作业平均完成时间是否符“双减”政策的要求，并说明理由．

查看解析收藏纠错

+选题
2. 为培养学生良好的运动习惯，提高学生的身体素质，我校开展了“花样跳绳”和“春季长跑”等体育活动.体育老师随机抽取了八年级男、女各60名学生的长跑成绩，并将数据进行整理分析，给出了下面部分信息：
数据分为A，B，C，D四个等级，分别是：
A： $\text{[math]}$ ， B： $\text{[math]}$ ， C： $\text{[math]}$ ， D： $\text{[math]}$
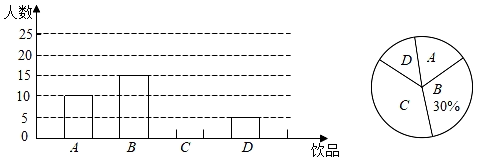
60名男生成绩的条形统计图以及60名女生成绩的扇形统计图如图：
男生成绩位于B等级前10名的分数为：
95，95，95，94，94，94，92，91，90，90.
60名男生和60名女生成绩的平均数，中位数，众数如下表：
性别
平均数
中位数
众数
男生
94
a
96
女生
95
94
96
根据以上信息，解答下列问题：

（1）填空： $\text{[math]}$ ， $\text{[math]}$ ；

（2）计算抽取的男生成绩在B等级的人数，并补全条形统计图；

（3）根据以上数据，你认为在此次活动中，男生成绩好还是女生成绩好？请说明理由（说明一条理由即可）．

（4）若该年级有800名学生，估计成绩为A等级的学生约为人．

查看解析收藏纠错

+选题
3. 如今很多初中生喜欢购买饮品饮用，既影响身体健康又给家庭增加不必要的开销，为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查，大致可分为四种：A：白开水，B：瓶装矿泉水，C：碳酸饮料，D：非碳酸饮料，根据统计结果绘制如下两个不完整的统计图，根据统计图提供的信息，解答下列问题：

（1）这个班级有 ▲ 名同学；并补全条形统计图；

（2）若该班同学每人每天只饮用一种饮品(每种仅限一瓶，价格如表)，则该班同学每天用于饮品的人均花费是多少元？

（3）在饮用白开水的同学中有4名班委干部，为了养成良好的生活习惯，班主任决定在这4名班委干部(其中有两位班长记为A，B，其余两位记为C，D)中随机抽取2名作为良好习惯监督员，请用列表法或画树状图的方法，求出恰好抽到2名班长的概率．

查看解析收藏纠错

+选题
4. 某校开展了以“不忘初心，牢记使命”为主题的知识竞赛，现从该校八、九年级各随机抽取10名学生的成绩进行整理，描述和分析（成绩用m表示），共分成四个组：A.80≤m＜85，B.85≤m＜90，C.90≤m＜95，D.95≤m≤100．另外给出了部分信息如下：
八年级10名学生的成绩：99，80，99，86，99，96，90，100，89，82．
九年级10名学生的成绩在C组的数据：94，90，94．
八、九年级抽取学生成绩统计表
年级
八年级
九年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4
根据以上信息，解答下列问题：

（1）上面图表中的a＝，b＝，c＝．

（2）扇形统计图中“D组”所对应的圆心角的度数为．

（3）根据以上信息，你认为哪个年级的学生对“不忘初心，牢记使命”的内容掌握较好？说明理由．（一条即可）

（4）该校九年级共有840名学生参加了知识竞赛活动，估计九年级参加此次知识竞赛活动成绩为较好（90≤m＜95）的学生有多少人？

查看解析收藏纠错

+选题
5. 作为全球最大的新能源汽车市场，混合动力、纯电动乃至氢燃料汽车，不但是中国出口的“金名片”和本土市场消费升级的新选择，而且正在加速成为经济高质量发展的新引擎.2022年1月，中国新能源汽车产销分别完成45.2万辆和43.1万辆，同比分别增长1.3倍和1.4倍，出口同比增长5.4倍．阳江市某中学的一个社团调查小组在本校学生中开展主题为“新能源汽车知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”“比较了解”“基本了解”和“不太了解”四个等级，划分等级后的数据整理如下表：
等级
非常了解
比较了解
基本了解
不太了解
频数
25
55
18
2
频率
0.25
m
0.18
0.02

（1）本次问卷调查取样的样本容量为，表中m的值为；

（2）根据表中的数据计算等级为“非常了解”的频数在扇形统计图（如图）中所对应的扇形的圆心角的度数，并补全扇形统计图；

（3）若该校有学生1500人，请根据调查结果估计这些学生中“非常了解”及“比较了解”新能源汽车知识的总人数约为多少？

查看解析收藏纠错

+选题
6. 已知矩形ABCD的边AB=21，BC=19，r是给定的小于1的正实数.

（1）在矩形ABCD内任意放入114个直径为1的圆.证明：在矩形ABCD内一定还可以放入一个直径为r的圆，它和这114个圆都没有交点（也不在某个圆的内部）；

（2）在矩形ABCD内任意放入95个单位正方形（边长为1的正方形）.证明：在矩形ABCD内一定还可以放入一个直径为r的圆，它和这95个正方形都没有交点（也不在某个正方形的内部）.

查看解析收藏纠错

+选题
7. 从2021年秋季开学以来，全国各地中小学都开始实行了“双减政策”．为了解家长们对“双减政策”的了解情况，从某校1200名家长中随机抽取部分家长进行问卷调查，调直评价结果分为“了解较少”“基本了解”“了解较多”“非常了解”四类，并根据调查结果绘制出如图所示的两幅不完整的统计图．

（1）本次抽取家长共有人，扇形图中“基本了解”所占扇形的圆心角是；

（2）估计此校“非常了解”和“了解较多”的家长共有多少人?

（3）学校计划从“了解较少”的家长中抽取1位初一学生家长，1位初二学生家长，2位初三学生家长参加培训，若从这4位家长中随机选取两人作为代表，请通过列表或面树状图的方法求所选出的两位家长既有初一家长，又有初二家长的概率．

查看解析收藏纠错

+选题

8. 为庆祝中国共产党建党100周年，某校开展了党史知识竞赛．某年级随机选出了一个班的初赛成绩进行统计，得到如下统计图表，已知在扇形统计图 $\text{[math]}$ 分数段对应的扇形六圆心角为 $\text{[math]}$ ．某校组织读书征文比赛活动，评选出一、二、三等奖若干名，并绘成如图所示的统计表和扇形统计图（不完整），请你根据图中信息解答下列问题：

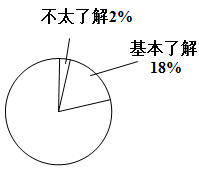
统计表

分段	成绩范围（分）	频数	频率
$\text{[math]}$	90~100	$\text{[math]}$	0.1
$\text{[math]}$	80~89	20	$\text{[math]}$
$\text{[math]}$	70~79	$\text{[math]}$	0.3
$\text{[math]}$	70分以下	10	$\text{[math]}$

注：90~100表示成绩 $\text{[math]}$ ，满足 $\text{[math]}$ ，以下相同．

扇形统计图

（1）在统计表中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；

（2）若该年级参加初赛的学生共有2000人，根据以上统计数据估计该年级成绩在90分及以上的学生人数；

（3）若统计表 $\text{[math]}$ 分数段的男生比女生少1人，从 $\text{[math]}$ 段中任选2人参加复赛，请用列表法或画树状图的方法，求出恰好抽到1名男生和1名女生的概率．

查看解析收藏纠错

+选题

9. 为了有效推进儿童青少年近视防控工作，某校积极落实教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案》，决定开设以下四种球类的课外选修课程：篮球、足球、排球、乒乓球，为了解学生需求，该校随机对本校部分学生进行了“你选择哪种球类课程”的调查（要求必须选择且只能选择其中一门课程），并根据调查结果绘制成如下不完整的统计图表．

课程

人数

篮球

m

足球

21

排球

30

兵乓球

n

（1）求m，n的值；

（2）求扇形统计图中“足球”对应扇形圆心角的度数；

（3）该校共有1800名学生，请你估计全校选择“乒乓球”课程的学生人数．

查看解析收藏纠错

+选题
10. 党的十八大以来，文山州牢固树立科学发展、绿色发展理念，把生态文明建设贯穿于经济、政治、文化和社会建设各个方面，深入实施“七彩云南文山保护行动”和“森林文山”建设．截止2017年底，全州共投入林业生态项目资金35亿元，完成了四项林业生态项目 $\text{[math]}$ 表示新一轮退耕还林，B表示石漠化治理，C表示天保工程森林管护，D表示天然商品林停伐 $\text{[math]}$ 的综合治理．并绘制出以下两幅不完整的统计图．请根据图中提供的信息，解答下列问题：

（1）此次林业生态项目共完成综合治理面积 ▲ 万亩．并将条形统计图补充完整；

（2）项目C占综合治理面积的百分比是多少？

（3）求扇形统计图中，项目D所对应的圆心角的度数．

查看解析收藏纠错

+选题
11. 4月23日是“世界读书日”，学校开展“整本书阅读”活动，以提升青少年的阅读兴趣.七年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计，根据所得数据绘制了两幅不完整统计图(每组包括最小值，不包括最大值).七年级(1)班每天阅读时间在0.5小时以内的学生占全班人数的8%.
根据统计图解答下列问题：

（1）七年级(1)班有名学生.

（2）补全频数直方图.

（3）除七年级(1)班外，七年级其他班级每天阅读时间在1~1.5小时的学生有165人，补全扇形统计图.

（4）求该年级每天阅读时间不少于1小时的学生有多少人?

查看解析收藏纠错

+选题
12. 为提高节水意识，小申随机统计了自己家7天的用水量，并分析了第3天的用水情况，将得到的数据进行整理后，绘制成如图所示的统计图.（单位：升）

（1）求这7天内小申家每天用水量的平均数和中位数；

（2）求第3天小申家洗衣服的水占这一天总用水量的百分比；

（3）请你根据统计图中的信息，给小申家提出一条合理的节约用水建议，并估算采用你的建议后小申家一个月（按30天计算）节约的用水量。

查看解析收藏纠错

+选题
13. 为了解某种电动汽车的性能，对这种电动汽车进行了抽检，将一次充电后行驶的里程数分为A，B，C，D四个等级，其中相应等级的里程依次为200km，210km，220km，230km，获得如下不完整的统计图。

根据以上信息，解答下列问题：

（1）这次被抽检的电动汽车共有多少辆？请补全条形统计图；

（2）估计这种电动汽车一次充电后行驶的平均里程数。

查看解析收藏纠错

+选题
14. 某市教育行政部门为了了解七年级学生每学期参加公益活动的情况，抽样调查了某中学学生一个学期参加公益活动的天数，并用得到的数据绘制了如图所示两幅不完整的统计图．

（1）扇形统计图中a的值是，该校七年级学生共有人；

（2）在该次抽样调查中，参加活动时间为5天的学生共有（）人，并补全条形统计图；

（3）如果该市七年级学生共有20000人，估计这20000人中，参加公益活动时间不少于4天的学生有多少人？

查看解析收藏纠错

+选题
15. 为庆祝五四青年节，学校计划在“五四”前夕举行班级歌咏比赛，要确定一首喜欢唱的人数最多的歌曲为每班必唱歌曲．为此提供代号为 $\text{[math]}$ $\text{[math]}$ 四首备选曲目让学生选择，经过抽样调查，并将采集的数据绘制成如下的两幅不完整的统计图．请根据图1，图2所提供的信息，解答下列问题：

（1）本次抽样调查的学生有多少名？

（2）请将条形统计图补充完整；

（3）求扇形图中 $\text{[math]}$ 的圆心角度数；

（4）由统计图发现喜欢唱的人数最多的歌曲为哪一首？若全校共有1200名学生，根据抽样调查的结果估计全校共有多少名学生喜欢唱此歌曲？

查看解析收藏纠错

+选题

16. 某中学积极开展跳绳锻炼，一次体育测试后，体育委员统计了全班同学单位时间的跳绳次数，列出了频数分布表和频数分布直方图，如图：

次数	频数
60≤x＜80
80≤x＜100	4
100≤x＜120	18
120≤x＜140	13
140≤x＜160	8
160≤x＜180
180≤x＜200	1

（1）补全频数分布表和频数分布直方图；

（2）样本数据中组距是，组数是；

（3）若规定跳绳次数不低于140次为优秀，求全班同学跳绳的优秀率是多少？

查看解析收藏纠错

+选题

17. “疫情远未结束，防疫绝不放松”.为了了解同学们掌握防疫知识的情况，增强防疫意识，某校举行了疫情防护知识测试活动，现从该校七、八年级各随机抽取20名学生的测试成绩（90分及以上为优秀）进行整理、描述和分析，以下是部分信息.
七年级20名学生的测试成绩：72，80，85，90，78，82，80，90，92，90，100，90，83，88，97，98，99，80，81，85.
八年级20名学生的测试成绩条形统计图如图：
【七、八年级抽取的学生的测试成绩的平均数、众数、中位数、90分及以上人数所占百分比如下表所示】：
年级
平均数
众数
中位数
90分及以上人数所占百分比
七年级
87
a
86.5
45%
八年级
87
94
b
c
根据以上信息，解答下列问题：

（1） a=、b=、c=；

（2）根据上述数据，你认为该校七、八年级中，哪个年级掌握防疫知识更好？请说明理由；

（3）该校七、八年级共有3000名学生参加了此次测试活动，估计参加此次测试活动成绩优秀的学生有多少人？

查看解析收藏纠错

+选题
18.

（1）已知四边形OBCA是平行四边形，点D在OB上．

①填空： $\text{[math]}$ ▲ ； $\text{[math]}$ ▲ ；

②求作： $\text{[math]}$ ．

（2）在一个不透明的袋子中装有（除颜色外）完全相同的红色小球1个，白色小球1个和黄色小球2个．
①如果从中先摸出一个小球，记下它的颜色后，将他放回袋子中摇匀，再摸出一个小球，记录下颜色，那么摸出的两个小球的颜色恰好是“一红一黄”的概率是；

②如果摸出的第一个小球之后不放回袋子中，再摸出第二个小球，这时摸出的两个小球的颜色恰好是“一红一黄”的概率是．

查看解析收藏纠错

+选题
19. 为了调查某小区居民的用水情况，随机抽查了若干个家庭3月份的用水量，结果如表：

月用水量（立方米）

10.5

14

16

18

户数

2

3

4

1

根据表格完成下列问题：

（1）写出这组数据的众数；

（2）求这若干个家庭3月份的平均用水量；

（3）请根据（2）的结论估计该小区1000个家庭3月份总用水量．

查看解析收藏纠错

+选题
20. 2021年是中国共产党成立100周年，某校组织开展了丰富多彩的主题教育活动，活动设置了A：诗歌朗诵表演，C：书画作品展览，D：手工作品展览，四个专项活动，学校随机抽取了部分学生进行调查，并根据调查结果绘制了如图所示的不完整的条形统计图和扇形统计图．

（1）本次随机调查的学生人数是．

（2）请你补全条形统计图；

（3）在扇形统计图中，“B”所在扇形的圆心角为度．

（4）若该校有学生1200人，则在这次活动中选择“A：诗歌朗诵表演”的学生有多少人？

查看解析收藏纠错

+选题

21. 为了让师生更规范地操作教室里的一体机设备，学校信息技术处制作了“教室一体机设备培训”视频，并在读报课时间进行播放．结束后为了解初中校部、高中校部各班一体机管理员对设备操作知识的掌握程度，得分用x（x为整数）表示，A：60≤x＜70，B：70≤x＜80，C：80≤x＜90，D：90≤x≤100，对得分进行整理分析，给出了下面部分信息：

初中一体机管理员的测试成绩在C组中的数据为：81，85，88．

高中一体机管理员的测试成绩：76，83，71，100，81，100，82，88，95，90，100，86，89， 93，86．

成绩统计表如下：

学部	平均数	中位数	众数
初中	88	a	98
高中	88	88	b

（1） a＝，b＝．

（2）通过以上数据分析．你认为 ▲ （填“初中”或“高中”）的一体机管理员对一体机设备操作的知识掌握的更好，请写出理由；

（3）若初中校部有100名一体机管理员，高中校部有140名一体机管理员，请估计此次浏试成绩达到90分及以上的一体机管理员共有多少人？

查看解析收藏纠错

+选题

22. 为“弘扬美食文化，助力黔菜出山”，某数学兴趣小组在云岩广场随机抽取500位云岩区市民填写了“舌尖上的贵阳——我最喜爱的贵阳小吃”调查问卷，兴趣小组将调查问卷整理后绘制成如下统计图，请根据所给信息解答以下问题：

（1）请补全条形统计图；

（2）已知云岩区人口约100万人，请估计云岩区市民中最喜欢“老素粉”的有多少万人？

（3） “五·一”小长假期间，来筑旅游的小度要从以上四种小吃中随机选择两种不同的小吃进行品尝，请用列表或画树状图的方法，求他选中“肠旺面”和“豆腐果”的概率.

查看解析收藏纠错

+选题
23. 中央电视台举办的“中国汉字听写大会”节目受到中学生的广泛关注．某中学为了了解学生对观看“中国汉字听写大会”节目的喜爱程度，对该校部分学生进行了随机抽样调查，并绘制出如图所示的两幅统计图．在条形图中，从左向右依次为：A类（非常喜欢），B类（较喜欢），C类（一般），D类（不喜欢）．已知A类和B类所占人数的比是 $\text{[math]}$ ，请结合两幅统计图，回答下列问题：

（1）本次抽样调查的样本容量是；

（2）求出B类的学生人数；

（3）扇形统计图中D类（一般）的圆心角度数为度．

查看解析收藏纠错

+选题
24. 我市某化工厂从2008年开始节能减排，控制二氧化硫的排放 $\text{[math]}$ 图 $\text{[math]}$ ，图 $\text{[math]}$ 分别是该厂 $\text{[math]}$ 年二氧化硫排放量 $\text{[math]}$ 单位：吨 $\text{[math]}$ 的两幅不完整的统计图，根据图中信息回答下列问题．

（1）该厂 $\text{[math]}$ 年二氧化硫排放总量是吨；这四年平均每年二氧化硫排放量是吨 $\text{[math]}$

（2）把图中折线图补充完整．

（3） 2008年二氧化硫的排放量对应扇形的圆心角是度，2011年二氧化硫的排放量占这四年排放总量的百分比是．

查看解析收藏纠错

+选题
25. 某学校组织了“热爱宪法，捍卫宪法”的知识竞赛，赛后发现所有学生的成绩（总分100分）均不低于50分，为了解本次竞赛的成绩分布情况，随机抽取若干名学生的成绩作为样本进行整理，并绘制了不完整的统计图表，请你根据统计图表解答下列问题．
学校若干名学生成绩分布统计表
分数段（成绩为x分）
频数
频率
50≤x＜60
16
0.08
　60≤x＜70
a
0.31
　70≤x＜80
72
0.36
　80≤x＜90
c
d
　90≤x≤100
12
b

（1）此次抽样调查的样本容量是　　；

（2）写出表中的a＝　　， b＝　　， c＝　　；

（3）补全学生成绩分布直方图；

（4）比赛按照分数由高到低共设置一、二、三等奖，若有25%的参赛学生能获得一等奖，则一等奖的分数线是多少？

查看解析收藏纠错

+选题
26. 某学校在暑假期间开展“心怀感恩、孝敬父母”的实践活动，倡导学生在假期中帮助父母干家务．开学以后，校学生会随机抽取了部分学生，就暑假“平均每天帮助父母干家务所用时长”进行了调查，以下是根据相关数据绘制的统计图的部分．
根据上述信息，回答下列问题：

（1）在本次随机抽取的样本中，调查的学生人数人；

（2）补全频数分布直方图；

（3）如果该校共有学生1000人，请你估计“平均每天帮助父母家务的时长不少于30分钟”的学生大约有多少人？

查看解析收藏纠错

+选题
27. 在抛物线 $\text{[math]}$ 中，规定：（1）符号 $\text{[math]}$ 称为该抛物线的“抛物线系数”；（2）如果一条抛物线与 $\text{[math]}$ 轴有两个交点，那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
完成下列问题：

（1）若一条抛物线的系数是 $\text{[math]}$ ，则此抛物线的函数表达式为，当 $\text{[math]}$ 满足时，此抛物线没有“抛物线三角形”；

（2）若抛物线 $\text{[math]}$ 的“抛物线三角形”是等腰直角三角形，求出抛物线系数为 $\text{[math]}$ 的“抛物线三角形”的面积；

（3）在抛物线 $\text{[math]}$ 中，系数 $\text{[math]}$ 均为绝对值不大于 $\text{[math]}$ 的整数，求该抛物线的“抛物线三角形”是等腰直角三角形的概率.

查看解析收藏纠错

+选题

28. 9月16日，2020线上智博会举行西部（重庆）科学城新闻发布会.会上透露，西部（重庆）科学城是“科学家的家、创业者的城”，力争到2035年，全面建成具有全国影响力的科技创新中心核心区.为了解民众对科学城相关知识的知晓程度，某公司派甲、乙两人各随机调查20名群众，填写了对科学城相关知识的调查问卷（满分为10分），得分用x表示（x为整数），数据分组为 A：0≤x＜2，B：2≤x＜4，C：4≤x＜6，D：6≤x＜8，E：8≤x≤10）.对问卷得分进行整理分析，给出了下面部分信息：

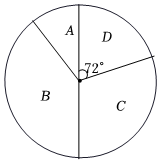
甲问卷得分的扇形统计图

乙问卷得分频数分布直方图（人数）

两组问卷得分的平均数，中位数，众数，满分率如下表：

	平均数（分）	中位数（分）	众数（分）	满分率
甲公司	5.15	n	6	5%
乙公司	5.55	6	P	5%

甲公司B组占10%，E组占30%，A圆心角度数 $\text{[math]}$ ；

甲公司分数在C、D组的数据为：6，4，4，6，6，7，6，5；乙公司E组所有数据之和为58.

根据以上信息，解答下列问题：

（1）扇形统计图中 $\text{[math]}$ ＝度，信息表中的中位数n＝分，众数P＝分；

（2）通过以上数据分析，你认为公司问卷调查的成绩更好，理由是；（写一条即可）

（3）若分数大于等于6即为合格，请估计问卷调查1600名群众中合格的人数是多少？

查看解析收藏纠错

+选题

29. 县某初中兴趣小组在实践课上计划用所学到的知识测量学校附近一楼房的高度，由于到楼房底部的水平距离不易测量，他们通过实地观察、分析，制订了可行的方案，并进行了实地测量．已知楼房 $\text{[math]}$ 前有一斜坡 $\text{[math]}$ ，它的坡度 $\text{[math]}$ ．他们先在坡面 $\text{[math]}$ 处测量楼房顶部 $\text{[math]}$ 的仰角 $\text{[math]}$ ，接着沿坡面向下走到坡脚 $\text{[math]}$ 处，然后向楼房的方向继续行走至 $\text{[math]}$ 处，再次测量楼房顶部 $\text{[math]}$ 的仰角 $\text{[math]}$ ，并测量了 $\text{[math]}$ 、 $\text{[math]}$ 之间的距离，最后测量了坡面 $\text{[math]}$ 、 $\text{[math]}$ 之间的距离．为了减少测量误差，小组在测量仰角以及距离时，都分别测量了两次并取它们的平均值作为测量结果（测角仪高度忽略不计），如下表：

项目	内容
课题	测量学校附近楼房的高度
测量示意图			说明：测点D、E与点C、B都在同一水平面上
测量数据	测量项目	第一次		第二次	平均值
	仰角 $\text{[math]}$ 的度数	30.2°		29.8°	30°
	仰角 $\text{[math]}$ 的度数	60.1°		59.9°	60°
	$\text{[math]}$ 、 $\text{[math]}$ 之间的距离	5.1米		4.9米	5米
	$\text{[math]}$ 、 $\text{[math]}$ 之间的距离	9.8米		10.2米
…	…

（1）任务一：两次测量 $\text{[math]}$ ， $\text{[math]}$ 之间的距离的平均值是米；

（2）任务二：请你帮助该小组根据上表中的测量数据，求出学校附近楼房 $\text{[math]}$ 的高．（结果精确到0.1米．参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题

30. 由于疫情的影响，学生不能返校上课，某校在直播授课的同时还为学生提供了四种辅助学习方式：A网上自测，B网上阅读，C网上答疑，D网上讨论。为了解学生对四种学习方式的喜欢情况，该校随机抽取部分学生进行问卷调查，规定被调查学生从四种方式中选择自己最喜欢的一种，根据调查结果绘制成如图两幅不完整的统计图：
根据统计图提供的信息，解答下列问题：

（1）本次共调查了名学生；并请补全条形统计图；

（2）在扇形统计图中，m的值是，D对应的扇形圆心角的度数是；

（3）若该校共有2000名学生，根据抽样调查的结果，请你估计该校最喜欢方式D的学生人数。

查看解析收藏纠错

+选题

每天书面完成时间t/分钟	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
人数	2	10	15	17	6

八、九年级抽取学生成绩统计表
年级	八年级	九年级
平均数	92	92
中位数	93	b
众数	c	100
方差	52	50.4

等级	非常了解	比较了解	基本了解	不太了解
频数	25	55	18	2
频率	0.25	m	0.18	0.02

分数段（成绩为x分）	频数	频率
50≤x＜60	16	0.08
60≤x＜70	a	0.31
70≤x＜80	72	0.36
80≤x＜90	c	d
90≤x≤100	12	b

性别	平均数	中位数	众数
男生	94	a	96
女生	95	94	96

课程	人数
篮球	m
足球	21
排球	30
兵乓球	n

月用水量（立方米）	10.5	14	16	18
户数	2	3	4	1

备考浙教版中考数学题型专项训练 统计与概率 解答题专练

一、综合题

相关试卷 收起∨

备考浙教版中考数学题型专项训练统计与概率解答题专练

相关试卷收起∨